|
Soit
à extraire la racine carrée de 7 485 696.
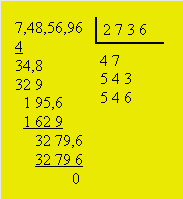
1.
On partage le nombre donné en tranches de deux chiffres à partir de la droite
comme ceci : 7,48,56,96.
2.
On extrait la racine carrée de 7 qui est dans la première tranche et on
conserve la partie entière du résultat qui est 2. On écrit 2 dans le crochet.
On élève 2 au carré. On inscrit 4 sous le 7 à gauche. La différence est 3.
On écrit ce chiffre sous le 4. Le premier chiffre de la racine carrée est 2.
3.
On abaisse 48 en ayant soin de conserver un seul chiffre dans la deuxième
tranche. On écrit 34,8. On double le premier chiffre de la racine
carrée : 2 × 2 = 4 et on l’écrit sous le crochet. On divise 34,8 par
4. On obtient 8. On écrit temporairement ce chiffre dans le crochet et sous le
crochet. On multiplie 48 et 8. On obtient 384. Ce nombre est supérieur à 348.
On efface donc les deux 8 qui viennent d’être écrits. On prend le chiffre
inférieur à 8, soit 7. On écrit ce chiffre dans et sous le crochet. Le
deuxième chiffre de la racine est 7.
4. On
multiplie 47 et 7. On obtient 329. On écrit ce résultat sous 34,8. On
soustrait. On obtient 19. On abaisse 56 en ayant soin de conserver un seul
chiffre dans la deuxième tranche : ce qui fait 195,6. On double le nombre qui
correspond aux deux premiers chiffres du nombre dans le crochet : 27 × 2 =
54. On l’écrit sous 47. On divise 195,6 par 54. On obtient 3 comme résultat.
On écrit ce chiffre dans et sous le crochet. Le troisième chiffre de la racine
est 3.
5.
On multiplie 543 et 3. On obtient 1629. On écrit ce résultat sous 195,6. On
soustrait. On obtient 327. On abaisse 96 en ayant soin de conserver un seul
chiffre dans la deuxième tranche : ce qui fait 3279,6. On double le nombre
qui correspond aux trois premiers chiffres dans le crochet : 273 × 2 =
546. On l’écrit sous 543. On divise 3279,6 par 546. On obtient 6 comme
chiffre. On écrit ce chiffre dans le crochet et sous le crochet. On multiplie
5466 et 6. On obtient 32 796. On écrit ce résultat sous le 3279,6. On
soustrait. Le résultat est 0. Le quatrième chiffre de la racine est 6. La
racine carrée de 7 485 696 est 2736.
On
peut trouver la racine carrée d’un nombre par un procédé amusant mais peu
pratique. Il s’agit de soustraire successivement les entiers impairs
consécutifs à partir de 1 jusqu'à ce que le dernier résultat soit inférieur
au terme soustrait. Le nombre d’opérations est la valeur entière de la
racine carrée. Si on veut extraire la racine carrée de 75, on peut calculer
ainsi :
75 - 1 = 74 74 - 3 =
71 71 - 5 =
66 66 - 7 = 59
59 - 9 = 50 50 - 11 = 39
39 - 13 = 26 26 - 15 = 11
Parvenu
à 11, on a effectué huit opérations. Alors, la valeur entière de la racine
carrée est 8.
Une autre façon plus amusante que pratique de trouver la racine carrée d’un
nombre est de faire des divisions successives et de calculer la moyenne
arithmétique. Soit à extraire la racine carrée de 563 798. Comme on l’a
expliqué précédemment, la racine carrée a trois chiffres.
1.
On recherche le premier chiffre de la racine carrée. C’est la racine carrée
de la première tranche. La racine carrée entière de 56 est 7.
2.
On divise le nombre donné par 700, soit 7 suivi de deux zéros puisque la
racine carrée a trois chiffres. On fait 563 798 ÷ 700 = 805.
3.
On prend la moyenne arithmétique de 700 et de 805 qu’on arrondit. On fait
(700 + 805) ÷ 2 = 753.
4.
On divise 563 798 par 753. On obtient approximativement 749.
5.
On prend la moyenne arithmétique de 753 et de 749. On obtient 751. D’où, la
racine carrée de 563 798 est approximativement 751.
Si on veut une
plus grande précision, on continue en répétant les mêmes opérations ou
encore on n’arrondit pas les résultats.
© Charles-É. Jean
Index
: C
|
![]()
![]()