Cubique

° Racine cubique. – Nombre qui multiplié trois fois par lui-même donne un cube. Ainsi 7 est la racine cubique de 343, car 7 × 7 × 7 = 343 = 7³. Quand la racine cubique est un entier, le cube est dit parfait. Pour trouver le nombre de chiffres d’une racine cubique, on partage le nombre à extraire en tranches de trois chiffres ; on compte le nombre de tranches, y compris celle d’un ou de deux chiffres. Le nombre de tranches correspond au nombre de chiffres de la racine. 

Aussi la racine cubique de 82 314 203 est formée de trois chiffres. La racine d’un nombre inférieur à 1000 a un chiffre ; celle d’un nombre variant de 1000 à 999 999 est composée de deux chiffres ; celle d’un nombre variant de 1 000 000 à 999 999 999 est composée de trois chiffres. On peut extraire la racine cubique d’un entier sans l’aide d’un instrument de calculs. 

Au lieu de décrire un algorithme général, on donne un exemple. Soit à extraire la racine cubique de 82 314 203.

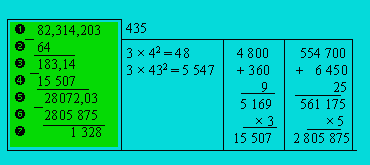
Œ On sépare le nombre donné en tranches de trois chiffres à partir de la droite. La tranche de gauche peut avoir trois chiffres ou moins.

� On cherche le plus grand cube parfait inférieur à 82. C’est 64 dont la racine est 4. On écrit 4 dans le crochet de droite. On écrit 64 sous 82.

Ž  On fait 82 - 64 = 18. On abaisse la tranche suivante, soit 314. On sépare les deux derniers chiffres par une virgule à partir de la droite. On a donc 183,14.

� On triple le carré de la racine, ce qui fait 3 × 4² = 48. On se demande le nombre de fois que 48 est dans 183. Il y est 3 fois. On vérifie si le chiffre 3 est bon. Pour cela, on multiplie 48 par 100, ce qui donne 4800. On multiplie le triple de la racine (3 × 4 = 12) par le chiffre à vérifier (3), puis par 10, ce qui fait 12 × 3 × 10 = 360. On élève au carré le chiffre à vérifier, ce qui donne 9. On additionne 4800, 360 et 9, ce qui donne 5169. On multiplie ce résultat par le chiffre à vérifier, ce qui fait 5169 × 3 = 15 507. Ce nombre est inférieur à 18 314. D’où, 3 est le deuxième chiffre de la racine. On écrit 3 dans le crochet. La racine est maintenant 43. On écrit 15 507 sous 18 314.

� On fait 18 314 - 15 507 = 2807. On abaisse la troisième tranche, soit 203. On sépare les deux derniers chiffres par une virgule à partir de la droite. On a écrit 28072,03.

‘ On triple le carré de la racine, ce qui fait 3 × 43² = 5547. On se demande le nombre de fois que 5547 est dans 28 072. Il y est 5 fois. On vérifie si le chiffre 5 est bon. Pour cela, on multiplie 5547 par 100, ce qui donne 554 700. On multiplie le triple de la racine (3 × 43 = 129) par le chiffre à vérifier (5), puis par 10, ce qui fait 129 × 5 × 10 = 6450. On élève au carré le chiffre à vérifier, ce qui donne 25. On additionne 554 700, 6450 et 25, ce qui donne 561 175. On multiplie ce résultat ce résultat par le chiffre à vérifier, ce qui fait 561 175 × 5 = 2 805 875. Ce nombre est inférieur à 2 807 203. D’où, 5 est le troisième chiffre de la racine. On écrit 5 dans le crochet. La racine est 435. On écrit 2 805 875 sous 2 807 203.

’ On fait 2 807 203 - 2 805 875 = 1328. Le reste est 1328.

La racine cubique de 82 314 203 est 435, reste 1328. Si on obtient 0 comme chiffre possible de la racine, on ne fait qu’abaisser une autre tranche et on continue. Si un chiffre possible de la racine est trop grand, on vérifie un chiffre plus petit. Dans le cas où il dépasse 9, on essaie 9. 

En faisant le cube de la racine, auquel on additionne le reste, on retrouve le nombre à extraire.

© Charles-É. Jean

Index : C