Aide-mémoire Ensemble

Ensemble

Groupe d'objets distincts qui forment un tout. Les élèves d’une école forment un ensemble. La propriété commune, soit d'être de la même école, permet de considérer toutes ces personnes dans un même ensemble. Maryse, Natacha et Simon sont trois élèves de l'école Bon-Accueil. Chacun appartient à cet ensemble ou encore est un élément de cet ensemble.

On désigne généralement un ensemble par une lettre majuscule et un élément par une minuscule. Soit E l'ensemble des élèves de l'école Bon-Accueil et m mis pour Maryse, n pour Natacha et s pour Simon, on écrira : m Î E, n Î E et s Î E. Le symbole Î est un signe d'appartenance. Il signifie appartient à ou encore est un élément de.

Supposons que Bernard n'est pas un élève de l'école Bon-Accueil. Alors, il n'appartient pas à l'ensemble E. Si on pose b pour Bernard, alors on écrira b Ï E. On peut noter un ensemble de deux façons : par énumération et en compréhension.

Par énumération
On dresse alors la liste de tous les éléments qui composent cet ensemble. On écrit les éléments en les encadrant par des accolades et en les séparant l'un à l'autre par une virgule. L'ensemble A des chiffres arabes s'écrira : A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 0}.

Dans un ensemble, chaque élément est écrit une seule fois. L'ordre dans lequel les éléments apparaissent n'a pas d'importance. L'ensemble B des lettres du mot patente pourra être noté : B = {p, a, t, e, n}. On peut utiliser les points de suspension. Cela signifie alors que d'autres éléments existent ; mais que ce serait trop long de tous les énumérer.

On pourra noter ainsi l'ensemble A des lettres de l'alphabet : A = {a, b, c, d, e, f, ..., x, y, z}. L'ensemble D des nombres pairs pourra s'écrire : D = {2, 4, 6, 8, 10, 12, 14, ...}.

En compréhension
On énonce alors la ou les propriétés qui caractérisent l'ensemble en choisissant la variable x comme représentant chacun des éléments.

L'ensemble A des chiffres arabes sera alors noté : A = {x | x est un chiffre arabe}. On lira : A est l'ensemble de tous les éléments x tels que x est un chiffre arabe. Le symbole | se lit : tels que. L'ensemble B des mois de l'année sera écrit ainsi en compréhension. B = {x | x est un mois de l'année}. Cette notation est utile quand certains éléments sont inconnus ou que la liste est trop longue.

Trois situations peuvent se présenter quand on compare deux ensembles.
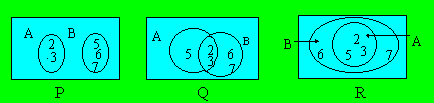
1. Les deux ensembles n'ont pas d'élément commun. Soit A = {2, 3}et B = {5, 6, 7}, aucun élément de A n'appartient à B et aucun élément de B n'appartient à A (figure P ci-après).

2. Certains éléments d'un premier ensemble appartiennent au second, les autres non. Soit A = {2, 3, 5} et B = {2, 3, 6, 7}, deux éléments sont communs. En effet, 2 appartient à A et à B ; de même 3 appartient à A et à B. On dit que les deux ensembles ont une intersection commune (figure Q).

3. Tout élément d'un premier ensemble appartient au second. Soit A = {2, 3, 5} et B = {2, 3, 5, 6, 7}, tout élément de A appartient à B. On dit que A est inclus dans B (figure R).

Index : E