|
Graphique
Une relation peut être représentée notamment par un
graphique sagittal, par un graphique cartésien ou par un diagramme cartésien.
Graphique sagittal
Graphique formé par deux diagrammes de
Venn. Des lignes munies d'un sens, appelées flèches, relie des éléments des
deux diagrammes. Par convention, l'ensemble de départ est celui d'où partent
les flèches. Soit A = {2, 5, 6, 9},
B = {1, 4, 5, 8, 11} et la
relation "est plus petit que", le graphique sagittal est :
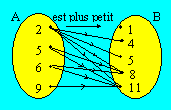
Le graphe de cette relation est : {(2,
4), (2, 5), (2, 8), (2, 11), (5, 8), (5, 11), (6, 8), (6, 11), (9, 11)}.
Graphique cartésien
Grille dans laquelle chaque droite est
à égale distance l'une de l'autre autant horizontalement que verticalement. On
identifie par un point les couples qui vérifient la relation. Soit A = {1,
3, 6, 9,11}, B = {2, 4, 7,
9, 12} et la relation "est plus petit que",
le graphique cartésien est :
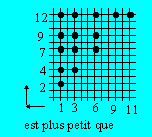
Le graphe de cette relation est {(1,
2), (1, 4), (1, 7), (1, 9), (1, 12), (3, 4), (3, 7), (3, 9), (3, 12), (6, 7),
(6, 9), (6, 12), (9, 12), (11, 12)}.
Diagramme cartésien
Tableau à double entrée qui
représente une relation entre les éléments d’un ensemble de départ et ceux
d’un ensemble d'arrivée. Les éléments d'un ensemble sont écrits à gauche
et les éléments de l'autre ensemble en bas ou en haut. Une flèche indique le
sens dans lequel la relation doit être lue. La case où la relation s'applique
est marquée par un signe distinctif, soit par un x, par un oui ou par un non.
Voici un diagramme cartésien :
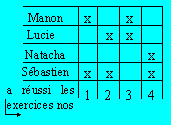
L'ensemble de départ est {Manon,
Lucie, Natacha, Sébastien}. L'ensemble d'arrivée
est {1, 2, 3, 4}. La
relation est "a réussi les exercices numéros". Le graphe de la relation
est : {(Manon, 1), (Manon, 3), (Lucie, 2), (Lucie,
3), (Natacha, 4), (Sébastien, 1), (Sébastien, 2), (Sébastien, 4)}.
On peut donc lire que Manon a réussi les exercices nos 1 et 3, etc.
© Charles-É. Jean
Index
: G
|
|
![]()
![]()