|
« Les nombres se suivent, mais ne se ressemblent pas.»
La suite des nombres
entiers constitue la base de toute l’arithmétique. Elle permet, en effet, d’asseoir
un système qui quantifie les objets de façon si claire que la compréhension
du concept est partagée par tous les individus. Chacun sait ce que représente
10 dollars ; mais, il serait difficile de s’entendre sur la quantité
correspondante à plusieurs dollars.
Dans la nature, les
événements se succèdent souvent d’une façon constante. Ainsi, les heures
se suivent jusqu’à ce qu’un jour soit formé ; les minutes se suivent jusqu’à
ce qu’une heure soit formée, etc. Dans le calendrier scolaire, les jours de
classe sont identifiés jour 1, jour 2, jour 3, etc. Personne n’aurait l’idée
d’adopter une autre séquence.
Ainsi, l’ensemble
des nombres entiers consécutifs peut être écrit sous forme d’une suite
arithmétique. Chaque terme diffère alors du précédent d’une quantité
fixe, appelée raison. Dans la suite arithmétique 1, 2, 3, 4, ... , la raison
est 1. Comme nous le verrons plus loin, il est intéressant de considérer des
suites dont la « raison » n’est plus un nombre fixe mais plutôt une
autre suite. Nous les appellerons suites arithmétiques auxquelles nous
attribuons un degré.
1.0 Suite arithmétique de degré
0
La suite
arithmétique de degré 0 est formée par la répétition d’un seul même
nombre. Voici une telle suite : 3, 3, 3, 3, 3, ... Cette suite est sans
intérêt, car nous connaissons toujours le terme d’un rang quelconque.
2.0 Suite arithmétique
de
degré 1
Par définition, la
raison de la suite arithmétique de degré 1 est une constante non nulle. Les
suites arithmétiques de degré 1 sont habituellement appelées
progressions
arithmétiques. Les termes de cette suite sont transformés par l’addition
de cette constante. C’est donc dire que les différences successives des
termes d’une suite arithmétique de degré 1 forment une suite arithmétique
de degré 0. De même, la suite des différences successives des termes d’une
suite arithmétique de degré d formeront une suite arithmétique de
degré (d - 1).
Construisons, par
exemple, la suite arithmétique de degré 1 dont le premier terme est 10 et dont
la raison est 3. La voici : 10, 13, 16, 19, 22, ... Pour toute suite
arithmétique, nous aimerions trouver une expression donnant son ne
terme, noté xn. Dans l’exemple précédent, on a : xn
= 3n + 7. Pour expliquer comment trouver cette formule lorsque nous
connaissons les premiers termes de la suite, prenons, par exemple, la suite 8,
15, 22, 29, 36, ...
Une suite du premier
degré est toujours représentée par une équation de même degré. La formule
générale est : xn = an + b où a
et b sont des constantes. Appliquons, dans
cette équation, les valeurs correspondantes de n et de xn
.
On a : x1=
8 ; d’où, a × 1 + b = 8 (1)
x2 =
15 ; d’où, a × 2 + b = 15
(2)
Soustrayons (1) de
(2). Nous trouvons que a est égal à 7, puis b à 1. L’équation
est donc xn = 7n + 1. Connaissant cette équation, nous
pouvons identifier facilement le terme de tout rang. Ainsi, le 100e
terme est 701. Remarquons qu’il suffit de connaître les deux premiers termes
seulement d’une suite arithmétique du premier degré pour trouver l’équation
correspondante.
3.0 Suite arithmétique
de degré 2
Les suites
arithmétiques de degré supérieur à l’unité ne sont pas tellement connues,
car peu d’auteurs en ont traité. Pourtant les cas concrets sont très
nombreux.
Indiquons d’abord
que la raison d’une suite arithmétique de degré supérieur à l’unité n’est
pas une constante, mais les termes successifs d’une suite du degré
inférieur. Pour construire une suite arithmétique de degré 2, il nous faut un
premier terme et une suite arithmétique de degré 1. Par exemple, en partant
avec 1 et en utilisant la suite 2, 3, 4, 5, ... comme raison, nous obtenons la
suite de degré 2 suivante : 1, 3, 6, 10, 15, ...
Il est intéressant de noter que les nombres qui forment
cette suite sont dits triangulaires
et peuvent être représentés par un triangle de boules.
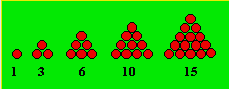
Le terme général d’une
suite arithmétique de degré 2 est un polynôme à coefficients entiers de
degré 2 en n, c’est-à-dire xn = an2
+ bn + c.
Exemple :
Trouvons l’équation correspondante à la suite 3, 5, 9, 15, 23, ...
Vérifions d’abord
le degré de la suite en faisant des différences successives.
3
5
9 15
23 ß degré
2
2 4
6
8
ß degré 1
2
2 2
ß degré 0 |
Dans l’équation de
forme générale, remplaçons n et xn par leur valeur
correspondante pour les trois premiers termes :
(1)
a + b
+ c = 3
(2) 4a + 2b
+ c = 5
(3) 9a + 3b
+ c = 9
En soustrayant (2) de
(3), puis (1) de (2), nous obtenons :
(4) 5a + b
= 4
(5) 3a + b
= 2
En soustrayant (5) de (4), nous trouvons a = 1 ; puis, par substitution, b = -1 et c
= 3. L’équation est : xn = n2
- n + 3.
Il suffit de
connaître les trois premiers termes d’une suite arithmétique de deuxième
degré pour trouver l’équation correspondante.
Le problème suivant
permet d’appliquer les connaissances acquises : « On partage un
cercle par des segments qui joignent deux points de la circonférence et qui se
coupent entre eux. En combien de parties au maximum peut-on diviser un cercle en
traçant 80 segments ? »
Faisons des
expériences de façon à voir la progression du nombre de parties en dessinant
successivement un segment de plus. Pour atteindre le maximum, coupons toujours
les segments tracés.
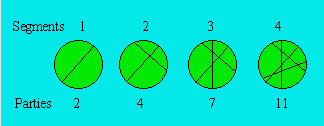
La suite 2, 4, 7, 11,
... est du deuxième degré. Vérifions les différences successives.
2
4
7 11
ß degré 2
2 3
4
ß
degré 1
1
1
ß
degré 0 |
Nous pouvons trouver
l’équation qui est : xn = (n2 + n
+ 2)/2.
(Voir Deux
problèmes de combinatoire par Jacques Labelle, Bulletin AMQ, 1978, vol.
XVIII, no 2, pp. 34-38)
Si n = 80,
alors xn = 3241. En traçant 80 segments dans un cercle, c’est
donc 3241 parties au maximum que nous pouvons obtenir.
4.0 Suite arithmétique
de degré 3
Écrivons une suite
qui commence par 7 et dont la raison est la suite du deuxième degré 2, 4, 7,
11, 16, ... Cette suite est : 7, 9, 13, 20, 31, 47, ...
Le terme général
est un polynôme de degré 3 en n : xn = an3
+ bn2 + cn + d. Pour trouver l’équation de
cette suite, remplaçons n et xn dans la formule
générale. Nous obtenons les quatre équations suivantes :
(1) a + b
+ c + d = 7
(2) 8a + 4b
+ 2c + d = 9
(3) 27a + 9b
+ 3c + d = 13
(4) 64a + 16b
+ 4c + d = 20
En résolvant ces
quatre équations, nous trouvons les valeurs de a, b, c et d.
L’équation de cette suite est : xn = (n2
+ 5n + 36)/6.
Maintenant, combien
peut-on compter de carrés de toute grandeur dans une grille carrée formée de
carrés unitaires ? Une des stratégies pour résoudre ce problème est de
faire le comptage dans des carrés réduits. Nous remarquerons alors une suite
de degré 3 et nous calculerons le 100e terme.
1 5
14
30 carrés
L’équation
de la suite est : xn = (2n3 + 3n2
+ n)/6.
5.0 Suite arithmétique
de degré d
Tout terme d’une
suite arithmétique de n’importe lequel degré d peut être
représenté sous forme d’un polynôme de même degré d que la suite.
Cette équation a la forme générale :
xn
= a1nd
+ a2 nd-1 + a3nd-2
+ ... + ad où a1, a2, a3,
... ad sont des constantes entières, n est le rang du
terme, d est le degré de l’équation et xn
représente de ne terme de la suite.
L’équation d’une
suite arithmétique de degré 4 est : xn = a1n4
+ a2n3 + a3n2
+ a4n + a5. Par exemple, si a1
= 3, a2 = 5, a3 = -2, a4 =
6 et a5 = -2, l’équation sera : xn =
3n4 + 5n3 - 2n2 + 6n
- 2. La suite correspondante est : 10, 90, 376, 1078, 2478, 4930, 8866, ...
Connaissant les
termes d’une suite arithmétique de degré d, nous pouvons trouver l’équation,
1. en identifiant le
degré de la progression ;
2. en écrivant l’équation
générale de même degré ;
3. en remplaçant n
et xn par leur valeur dans l’équation générale de degré d
de façon à trouver (d + 1) équations ;
4. en résolvant ces
équations pour trouver les coefficients du polynôme ;
5. en substituant ces
coefficients dans l’équation générale.
Nous pouvons
maintenant formuler les remarques suivantes :
1. Tout terme d’une
suite arithmétique de degré d peut être représenté par une équation
de degré d.
2. Pour pouvoir
trouver l’équation d’une suite arithmétique de degré d, il est
nécessaire de connaître les (d + 1) premiers termes.
3. Le degré d’une
suite arithmétique est déterminé par le calcul des différences successives
où le terme constant correspond à une suite de degré 0.
4. Lorsque nous
ajoutons un nouveau terme au début d’une suite, une autre équation
correspond à cette suite.
5. La somme
successive des deux premiers termes d’une suite, des trois premiers, des
quatre premiers, etc. engendre une autre suite de degré (d + 1).
6.0 Problèmes et recherche
6.1 Sur du papier
quadrillé, vous tracez le périmètre d’un carré de 2500 petits carrés.
Construisez de nouveau la grille en suivant les lignes, y compris le périmètre
du carré, en partant d’un sommet du grand carré. En aucun temps, le crayon
ne doit être levé et il n’est pas permis de passer deux fois sur une même
ligne. Quel est le maximum de carrés que vous allez construire de cette façon
?
6.2 Sylvain joue
chaque semaine à la loterie LOLO. Ses mises se présentent ainsi :
|
Sem.
1 |
Sem. 2 |
Sem. 3 |
Sem. 4 |
Sem.
5 |
Sem. 6 |
|
10 $ |
16 $ |
24 $ |
34 $ |
46 $ |
60 $ |
Combien Sylvain
misera-t-il, lors de la 204e semaine, si les mises progressent selon
la même règle ?
6.3 La suite des
nombres hexagonaux est : 1, 6, 15, 28, 45, ...
a) Quel est le 1000e
nombre hexagonal ?
b) Quelle est la
somme des 500 premiers nombres hexagonaux ?
6.4 Lors de sa 1e
journée de cueillette, Judith a ramassé 5 rameaux, la 3e journée
9 rameaux, la 6e journée 33 rameaux, la 10e journée 79
rameaux et la 15e journée 129 rameaux. En supposant que les jours de la cueillette
se suivent toujours selon une même règle et que le résultat de la cueillette
se fait selon une autre même règle, combien Judith aura-t-elle cueilli de
rameaux au cours de ses 50 premiers jours pendant lesquels elle a effectivement
ramassé des rameaux ?
6.5 Vérifier l’affirmation
suivante : Additionner les n premiers termes d’une suite de
degré d revient à trouver le terme de rang (n - 1) d’une autre
suite de degré (d + 1) dont les termes proviennent de l’addition
successive des deux premiers, des trois premiers, des quatre premiers termes,
etc. de la suite de degré d.
Û
_______
Article publié dans Bulletin
AMQ ( revue de l’Association mathématique du Québec), octobre 1985, p.
26 à 29.
|
![]()
![]()