Un problème vécu est constitué d’un ensemble d’éléments mis en place par la nature, par soi-même, par d’autres personnes ou par le hasard. C’est en pondérant et en conjuguant ces éléments connus ou appréhendés qu’on finit par maîtriser la situation et s’approcher de plus en plus de l’équilibre. Le problème disparaît alors pour laisser place à une nouvelle réalité qui est souvent la base d’un nouveau problème.

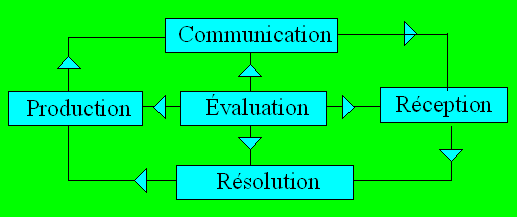
Dans une récréation, les éléments naissent de l’imagination ou sont tirés de la réalité. Le cycle de vie d’une récréation se présente en cinq étapes.

1. Une personne produit une récréation.

2. Elle la communique par des moyens divers comme la parole ou l’écrit.

3. La récréation est reçue par une autre personne.

4. Cette personne peut décider de résoudre la récréation donnée.

5. Un processus d’évaluation peut être appliqué à chacune de ces étapes.

Les cinq étapes sont illustrées dans ce schéma.

Dans cet article, nous traiterons de la production de récréations.

1. Éléments constitutifs d’une récréation
De façon générale, l’énoncé d’une récréation mathématique est constitué de trois éléments : les données initiales, les données conditionnelles ou conditions et l’inconnue.

1.1 Les données initiales
Dans l’énoncé d’une récréation, les informations qui sont la base ou le point de départ de la situation sont appelées données initiales. Elles sont exprimées par des nombres qui seront l’objet de calculs ou qui supportent une mesure, par des objets géométriques, par des événements, par des personnes. On peut identifier ces données lorsqu’on peut transformer le texte par des périphrases comme : à partir de, étant donné, connaissant, sachant que.

Problème 1. Un certain nombre d’amis se rencontrent à un restaurant pour prendre un repas. En vérifiant toutes les factures, Martine se rend compte que tout montant est composé des chiffres 1, 2, 3 et 4. La plus petite facture est alors de 12,34 $ et la plus grande de 43,21 $. Chaque convive a une facture de montant différent.

De combien de personnes ce groupe est-il composé ? (Les solutions sont données à la fin.)

Les données mathématiques initiales de cette récréation sont :
- les chiffres 1, 2, 3, 4 qui composent chaque montant
- les deux montants de 12,34 $ et de 43,21 $ qui déterminent les limites.

1.2 Les données conditionnelles ou conditions
Dans l'énoncé d'un problème, les données sont conditionnelles lorsque les informations viennent encadrer ou parfois restreindre les données initiales. Elles établissent un lien entre les données initiales et l’inconnue. On peut identifier les conditions lorsqu’on peut transformer le texte par des périphrases comme : si, en supposant que, lorsque, à la condition de, de telle manière que, de façon à. Ces données peuvent aussi correspondre à des restrictions sur la démarche ou sur les stratégies. Les conditions peuvent être parallèles ou dépendantes selon la relation qui existe entre elles.

Les conditions sont parallèles lorsqu’il n’y a pas de lien entre elles, comme l’illustre le schéma.

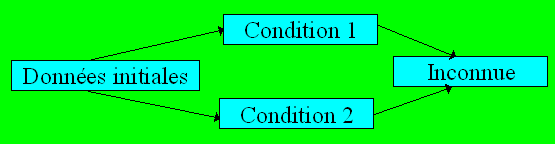
Problème 2. Marin et Vivien ont ensemble 1 001 $. Quatre fois l’avoir de Marin est égal à trois fois celui de Vivien. Quel montant d’argent possède Marin ?

Dans ce problème, les deux conditions sont tout à fait autonomes. On peut traduire chacune par une équation. Soit m l’avoir de Marin et v l’avoir de Vivien, on aura : m + v = 1001 et 4m = 3v. La résolution de ces deux équations permettra de déterminer l’avoir de Marin.

Les conditions sont dépendantes lorsque l’une est incluse dans l’autre. Dans ce cas, la condition principale précède la ou les conditions auxiliaires. Le schéma illustre cette situation.

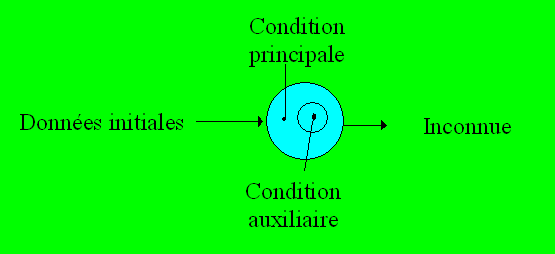
Problème 3. Mariette a planté quatre épinettes dans un terrain carré divisé en 16 parcelles comme ci-dessous :

Combien y a-t-il de petits terrains carrés qui sont composés de quatre parcelles et qui contiennent un seul arbre ?

Dans ce problème, les deux conditions sont :

1. Chaque petit terrain carré doit être composé de quatre parcelles.

2. Chaque petit terrain de quatre parcelles doit contenir un seul arbre.

La première condition seule donnerait un résultat de neuf terrains carrés ; la seconde lui en enlève quatre. On a donc appliqué cette dernière condition sur la première afin d’obtenir le résultat. De façon générale, une condition auxiliaire vient restreindre la portée de la condition principale.

1.3 L’inconnue
L’inconnue est une information qui est recherchée en appliquant les données conditionnelles sur les données initiales pour en tirer un élément qui était jusque-là non connu. Cet élément, c’est la réponse ou l’inconnue. L'inconnue est signifiée par une interrogation ou par la spécification d'une tâche. L’interrogation est exprimée par un adverbe ou un pronom interrogatif. La tâche est spécifiée par un verbe d'action. Le résultat recherché peut être notamment un nombre ou un ensemble de nombres, des figures géométriques, des mesures de toute sorte, des descriptions d’intervention ou de production, des personnages, etc.

2. Étapes de production d’une récréation
Composer une récréation consiste à rassembler des données initiales et des conditions qui, étant associées, peuvent permettre de préciser une inconnue à partir de situations vécues ou imaginées ou à partir d’une réalité mathématique simple ou complexe. Les données sont généralement présentées dans un texte. Ce dernier est parfois accompagné d’illustrations.

Une bonne récréation mathématique est un problème qui se présente sous une forme simple, dont la portée mathématique est le plus large possible et qui fait voir un certain attrait. Pour arriver à produire une bonne récréation, l’auteur devra adopter la démarche suivante :

1. Établir le niveau

2. Préciser les éléments notionnels

3. Déterminer le canevas

4. S’assurer de la faisabilité

5. Inventer un scénario

6. Réaliser la présentation

7. Évaluer le produit

Il est de bon aloi de réaliser toutes ces étapes en leur attribuant les meilleurs ingrédients et en en faisant une synthèse astucieuse. Certaines étapes peuvent se faire rapidement ou en concomitance avec d’autres, mais toutes demeurent essentielles.

2.1 Établir le niveau
Résoudre une récréation, c’est s’engager dans un processus qui vise à établir l’équilibre entre la personne et le problème. Composer une récréation, c’est établir et provoquer ce déséquilibre d’une façon harmonieuse et stimulante.

Au départ, le concepteur choisit le domaine de connaissances mathématiques qu’il veut aborder. Il définit un minimum d’habiletés mathématiques qui permettront une démarche efficace. Il s’efforce de pressentir les actions et les réactions de la personne qui s’engagera dans la résolution.

Une récréation est difficile si les connaissances nécessaires au dénouement sont trop grandes, si les habiletés requises ne sont pas suffisamment maîtrisées et si le problème suscite une attitude négative. Si la personne qui est confrontée au problème se rend compte que la difficulté est insurmontable, elle abandonnera.

Voilà pourquoi il faut viser à ce que l’amateur se sente à l’aise et ait le goût de s’aventurer. Bref, la récréation produit généralement un attrait en fonction de la difficulté qui y est perçue.

2.2 Préciser les éléments notionnels
Le choix des notions mathématiques ou logiques est essentiel au départ. En s’arrêtant dans un domaine précis comme l’arithmétique, la géométrie, les probabilités, l’analyse combinatoire, et en vulgarisant les notions, on donne à la récréation un caractère distinctif. Les critères qui vont guider l’auteur sont le souci de placer l’amateur en position raisonnable de défi.

À l’intérieur de chaque domaine, différents thèmes mathématiques peuvent être exploités. Encore là, il y aura un intérêt différent. Les récréations numériques, cryptarithmiques ou combinatoires seront vues d’une façon bien différente selon que l’on aime jouer avec les chiffres, avec les symboles ou avec les combinaisons.

La résolution de plusieurs récréations exige la manipulation d’opérations élémentaires comme l’addition, la soustraction, la multiplication et la division. Même là, en admettant que tous connaissent ces opérations, il n’est pas certain que l’amateur aura la patience ou le goût d’aligner des rangées de nombres et d’opérer sur eux. Il faut donc s’assurer que les données puissent être utilisées, s’il y a lieu en suggérant des raccourcis ou en indiquant des pistes relativement confortables.

Par ailleurs, il faut choisir, de préférence, des notions mathématiques qui s’appuient sur la vie courante. En même temps, on doit éviter de faire appel à des connaissances extérieures qui ne font pas partie du bagage commun à l’ensemble des individus.

Problème 4. Trouvez un nombre de cinq chiffres différents qui possède les propriétés suivantes :

Son premier chiffre est le nombre d’enfants de Lucifer.

Son deuxième chiffre est inférieur de 3 au premier et divisible par 4.

Son troisième chiffre est inférieur de 1 au premier.

Son quatrième chiffre est le nombre de béatitudes.

Son cinquième chiffre est inférieur de 4 au troisième.

Pour résoudre ce problème, il faut absolument connaître le nombre de béatitudes. Par ailleurs, même si quelqu’un ne connaît pas le nombre d’enfants de Lucifer, il pourra le trouver par déduction.

Pour certains, le nombre est un élément mystérieux à qui il est plaisant de faire faire des pirouettes ; pour d’autres, la ligne est un jouet polyvalent qui détermine des limites et à qui il est possible de donner la vie ; enfin, pour les esprits rationnels, rien n’est plus merveilleux qu’un édifice dont les éléments sont logiquement enchevêtrés et à partir desquels on peut en construire d’autres.

Notre forme d’intelligence va donc orienter notre choix envers l’une ou l’autre classe de récréations. Cela semble si vrai qu’en voyant une figure géométrique, certaines personnes vont immédiatement conclure : "ça c’est plaisant" ou "ça ne m’intéresse pas". Évidemment, des expériences antérieures, qui furent satisfaisantes ou pas, peuvent influencer leur attitude. Il est donc nécessaire de consentir une période d’exploration dans tous les domaines avant d’être certain de son choix.

C’est dans un contexte de connaissances de base qu’il faut poser la récréation. Ces connaissances sont souvent l’ossature du problème qui maximise son aspect récréatif.

2.3 Déterminer le canevas
Après avoir établi le niveau de la récréation et son contenu notionnel, l’auteur rassemble toutes les données mathématiques. Il met d’abord en place des données initiales soigneusement choisies et sur lesquelles il greffe des conditions. Il est possible que les données se révèlent alors trop nombreuses ou trop restreintes. On doit alors réduire ou élargir les données ou encore raffiner les conditions en les enrichissant ou en les rendant plus significatives.

Il s’agit là d’un travail captivant mais parfois difficile. L’ajout d’une seule condition peut détruire complètement le problème en rendant la solution trop évidente. Cet ajout peut, par ailleurs, agir sur les autres conditions et les placer dans un contexte inextricable.

En manipulant les données et les conditions, il arrive parfois que le concepteur a en tête une interrogation précise qui peut être le point de déclic du problème. Toutefois, compte tenu des données et des conditions posées, il peut devoir remplacer son interrogation par une autre plus restreinte notamment en fonction de la quantité de solutions. Il faut manifester suffisamment de souplesse pour oublier le canevas qu’on a imaginé et penser à l’intégration des données et des conditions en rapport avec une interrogation claire. On doit s’assurer que la transformation des données ne puisse pas se faire de façon mécanique. On doit aussi éviter d’introduire trop de conditions redondantes ou superflues.

Problème 5. Gaston et Luce ont ensemble 93 ans. Il y a 22 ans, Gaston était 11 ans plus jeune que Luce. De plus, il y a trois ans, la somme de leur âge était de 87 ans.

Quel est l’âge de chacun ?

Deux données sont superflues :  

1. Il y a 22 ans. 

2. Il y a trois ans, la somme de leur âge était 87 ans.

De façon générale, les informations données ne seront pas trop nombreuses. Dans certains cas, elles rendent le problème beaucoup trop facile et privilégient davantage une solution mécanique.

De plus, les conditions ne doivent pas être contradictoires. En effet, une situation dont les informations se contredisent peut devenir insoluble. Le détective, lui, est régulièrement confronté avec de tels problèmes et se voit obligé de sélectionner les informations qui lui apparaissent les plus vraisemblables, compte tenu de la validité des témoignages. Dans une récréation, des conditions contradictoires enlèvent de la valeur au problème, même si, dans certains cas, il est possible de répondre à l’interrogation.

Problème 6. Benoît et le père de Carl.

Noël est le fils de Martin.

Alcide est le père de Martin.

Benoît est le fils de Noël.

Carl est le père de Noël.

Qui est l’ancêtre ?

La deuxième proposition affirme que Martin est le père de Noël et la cinquième, que Carl est le père de Noël. Comme une personne ne peut avoir qu’un seul père, ces deux propositions sont contradictoires. Dans ce problème, il est quand même possible d’identifier l’ancêtre.

2.4 S’assurer de la faisabilité
Parvenu à cette étape, le concepteur doit s’intéresser aux stratégies éventuelles de résolution de la récréation. Les résultats de cette appréciation permettront d’établir la faisabilité du problème. Cette faisabilité peut être relative ou absolue. En effet, une récréation qui exigerait l’utilisation du calcul différentiel pour être résolue est faisable, mais peu accessible.

Par ailleurs, il se peut qu’une récréation soit vraiment non faisable même avec les meilleurs instruments connus. Cela peut surgir à la suite de l’introduction de données qui ne peuvent pas être agencées avec les conditions comme dans le cas suivant.

Problème 7. Placez les nombres 1, 3, 5, 6, 8, 10, 13, 15, 17 dans les cases d’un carré 3 ´ 3. La somme de trois nombres horizontalement, verticalement et en diagonale doit être 24.

Il est impossible de réaliser la tâche car la somme des données numériques devrait être 72 alors qu’elle est 78. L’amateur qui a peu d’expérience dans la formation de carrés magiques ne verra pas ce piège et cherchera en vain.

De façon générale, une récréation ne doit comporter qu’une seule réponse. Il peut arriver que l’information soit insuffisante et que cette situation engendre un nombre incalculable de réponses. Dans ce cas, le problème pourra être considéré comme déficient et il sera nécessaire d’imposer des conditions supplémentaires pour le rendre viable.

Problème 8. Un épicier prépare des sacs de navets et de carottes. Il compose des sacs de deux navets, puis des sacs de trois carottes. À la fin, il a empaqueté 50 légumes.

Combien a-t-il de sacs de navets et de carottes ?

Ce problème admet sept solutions qui sont numérotées dans ce tableau.

Comme il s’agit d’une situation réelle, il est préférable qu’il n’y ait qu’une seule réponse. Ce problème nécessite donc certaines corrections. On pourrait modifier la question. Par exemple, on pourrait demander le nombre de façons de faire ces empaquetages. En conservant la même question, on pourrait ajouter une donnée conditionnelle. Voici quelques conditions qui pourraient être intégrées au problème et le numéro de la réponse correspondante :

- Le produit du nombre de sacs de chaque sorte est 56. (1)

- Il y a cinq sacs de carottes de plus que ceux de navets. (2)

- Le nombre de sacs de chaque sorte est identique. (3)

- Le nombre de sacs est de 21. (4)

- Les nombres qui indiquent la quantité de sacs sont formés d’un seul même chiffre. (7)

- Il y a 11 fois plus de sacs de navets que de carottes. (7)

Certaines récréations admettent plus d’une réponse sans affecter la valeur de la question posée. Dans ce cas, celui qui résout le problème considère que la réponse trouvée satisfait aux exigences indiquées. Il ne sent ordinairement pas le besoin de colliger toutes les réponses possibles. Le carré latin suivant illustre cette situation.

Problème 9. Placez dans la grille carrée les nombres de 1 à 5. Deux nombres identiques ne doivent jamais apparaître dans une même rangée horizontale, verticale et diagonale.

Dans ce cas, dès que l’amateur atteint un bon résultat en concordance avec les données, pour lui, la récréation est résolue. De façon générale, on peut réduire le nombre de réponses à une, en demandant le plus petit, le plus grand, le minimum, le maximum, le premier, le dernier, celui du milieu, celui qui est au rang x, etc.

2.5 Inventer un scénario
Jusqu’à maintenant, le concepteur a identifié les données, les conditions et l’inconnue. Il s’est également assuré de la faisabilité du problème. Il doit donc imaginer un contexte qui peut être mathématique, réaliste ou imaginaire. Si le contexte est purement mathématique, il n’y a généralement pas de mise en place d’un scénario. Dans les deux autres cas, le concepteur peut imaginer des noms, des faits et des situations précises. Ce contexte doit être significatif et captiver l’intérêt.

Les lecteurs seront captivés par un scénario qui leur parle d’eux-mêmes et des objets qui les entourent. Ils se perdront dans des descriptions de lieux et de situations étrangères. Il est de bon aloi que le texte soit romancé et peut-être humoristique, qu’il comporte des noms, des faits et des situations précises. Il ne faut pas cependant verser dans un fouillis de détails que le lecteur a de la difficulté à discriminer. Toutes les propositions doivent, le plus possible, contenir des éléments susceptibles d’être traduits en langage mathématique.

L’histoire peut être embellie, mais avec une certaine parcimonie pour que la compréhension ne soit pas perturbée. En aucun temps, le lecteur ne doit s’interroger sur la pertinence des détails. Il faut donc éviter les mots superflus et les périphrases déroutantes. On croit que l’amateur réussit plus facilement à se détacher du problème si celui-ci est dans un contexte imaginaire.

Exercez-vous à identifier les informations inutiles dans cette récréation.

Problème 10. Ce soir-là, après une dure journée de labeur, Érica se mit à compter les moutons. Nul ne sut jamais combien elle en compta . Sauf qu’au cours d’un rêve, elle entendit une voix qui disait : "Je suis le compteur officiel de moutons pour le grand dieu Dantonlit. Je t’annoncerai, à travers mes paroles, le nombre de moutons que tu as vu défiler. C’est le carré d’un nombre entier. Si tu fais la différence entre ce carré et le carré du nombre précédent, tu obtiens un autre carré qui a un nombre de chiffres identique à celui des oreilles d’un mouton. N’oublie pas de me remercier mais à l’avenir, au lieu de compter des moutons jusqu’à un nombre de chiffres identiques au nombre de pattes d’un mouton, essaie plutôt de dénouer un labyrinthe qui contient autant de chemins impairs."

Érica se mit à aligner des chiffres. Finalement, elle identifia le nombre de moutons que, dans son rêve, elle avait comptés. Quel est ce nombre ?

Ce problème sera sans doute déroutant parce qu’il contient un grand nombre d’informations et que, de plus, il ne contient aucun nombre, du moins à première vue.

Les cinq récréations suivantes contiennent globalement les mêmes données initiales, les mêmes conditions et la même inconnue. La première récréation est dans un contexte mathématique, les trois autres dans un contexte réaliste et la dernière dans un contexte imaginaire.

Problème 11. La somme de deux nombres est 48. Leur différence est 8.

Quels sont ces deux nombres ?

Problème 12. Ce jour-là, Martin et Martine ont parcouru à eux deux 48 kilomètres en bicyclette. Martine en a parcouru huit de plus que Martin.

Quelle est la distance parcourue par chacun ?

Problème 13. La perche à la main, Pierre et Pierrette cueillent des pommes. En même temps, chacun met une pomme dans son panier. Pendant que Pierre s’arrête pour se désaltérer, Pierrette cueille huit pommes. Au retour, chacun compte ses pommes. À eux deux, ils en ont 48.

Combien chacun a-t-il cueilli de pommes ?

Problème 14. Quand Louis est né, Valérie avait huit ans. Un jour, ils se rencontrèrent. Louis lui dit :
- Quand nous aurons vécu 48 ans au total, nous irons faire un voyage en Europe.

Quel âge chacun aura-t-il lors de ce voyage ?

Problème 15. Deux seigneurs Cardio et Vasculo achètent en tout 48 robots destinés à provoquer la pluie. Dans un tunnel souterrain, Cardio aligne ses robots en une rangée. Vasculo fait de même en plaçant chacun de ses robots à côté d’un robot de Cardio. Il se rend compte que huit robots ne peuvent pas être associés à ceux de son compère.

Combien chacun a-t-il acheté de robots ?

Composer un problème dans un contexte imaginaire exige généralement plus de mots. Par ailleurs, la difficulté de composition vient du fait que la plupart des mots utilisés sont des mots réels à qui on veut donner une signification irréelle.

D’un même canevas, peuvent naître plusieurs récréations dont la solution est identique. Voici deux exemples qu’il est intéressant de comparer :

Problème 16. Ils sont trois hommes avec chacun sa femme qui veulent passer une rivière et n’ont qu’un petit bateau auquel ne peuvent passer plus de deux personnes à la fois. Or il est ainsi ordonné entre eux que nulle de leurs femmes ne se doit trouver avec un autre homme que son mari si celui-ci n’est pas présent en deçà de la rivière ni en delà. Autrement cette femme est réputée déshonnête et déloyale à son mari.

L’on demande maintenant comment ces six personnes pourront passer la rivière, l’honneur des femmes étant sauf. (Nicolas Chuquet dans Triparty en la science des nombres)

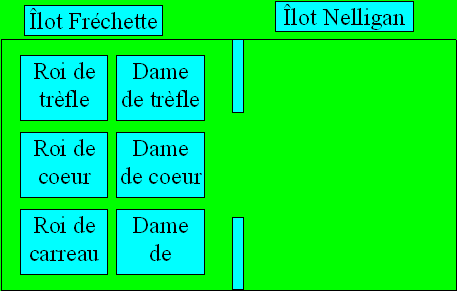
Problème 17. Faites passer les six cartes de l’îlot Fréchette à l’îlot Nelligan en respectant les conditions suivantes :

M Au plus, deux cartes à la fois peuvent emprunter le corridor dans un sens ou dans l’autre.

M Les déplacements se font successivement de l’îlot Fréchette à l’îlot Nelligan et de l’îlot Nelligan à l’îlot Fréchette.

M Aucun roi ne peut traverser en compagnie d’une dame autre que celle de sa famille.

M Pour pouvoir demeurer avec des dames dans un îlot, un roi doit être accompagné de la dame de sa famille.

2.6 Réaliser la présentation
Le temps est venu d’écrire le texte et de produire les illustrations. C’est là une tâche très délicate et très importante qui exige beaucoup d’attention car le souci de produire une œuvre ayant des facettes attrayantes doit constamment guider le concepteur.

Lorsque l’amateur feuillette un livre de récréations mathématiques, son premier regard est souvent attiré par l’accessoire du problème c’est-à-dire le texte et les illustrations. Ces deux points sont, en effet, importants pour permettre un accrochage.

Des illustrations sont parfois intégrées au problème comme dans les figures magiques, les labyrinthes et les nombres croisés. Généralement, elles se présentent sous forme d’une grille, d’un diagramme ou d’un dessin. Elles donnent des informations supplémentaires parfois essentielles. Dans certains cas, le diagramme sera utilisé pour résoudre le problème. Dans d’autres cas, en plus d’être un élément visuel attrayant, le diagramme servira simplement à écrire la réponse.

Problème 18. Dans les cercles, placez les nombres 1, 3, 4, 5, 7, 7, 8, 9 et 11. La somme des nombres des cercles reliés par une même droite doit être égale à 16.

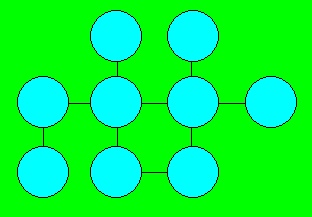
Les non-initiés des récréations mathématiques sont souvent arrêtés par la difficulté de comprendre le texte proposé. Cela peut être dû autant à l’auteur qu’à celui qui résout le problème. Du côté de l’auteur, on peut retrouver l’emploi d’un vocabulaire trop recherché ou inexact, l’emploi de termes techniques, une trop grande concision ou une trop grande verbosité. Pour sa part, l’amateur peut avoir une certaine difficulté à lire un texte, à comprendre certains mots, à faire le lien entre les éléments du problème ou à interpréter les données. On voit donc que l’énoncé doit être concis ; mais également on doit éviter des interprétations en explicitant les principaux termes.

Toutes les fois que c’est possible, il est recommandé d’écrire le texte au présent. Par ailleurs, les phrases courtes sont de bon aloi. Dans certains cas, on peut couper une phrase en deux. Par exemple, au lieu d’écrire : "Placez les nombres dans la grille de sorte que la somme soit 45 dans chaque rangée.", on pourrait écrire :  "Placez les nombres dans la grille. La somme doit être 45 dans chaque rangée."

L’usage de prénoms est un élément accrocheur. Au lieu d’écrire : "Un marchand a acheté ...", on peut écrire : "Pierrette a acheté ...". Parfois, il s’avère nécessaire d’aider à la compréhension par un exemple. Cela peut éviter de longues explications qui embrouilleraient l’énoncé du problème.

2.7 Évaluation du produit
Avant de rendre publique sa récréation, le concepteur doit en évaluer sa qualité. La qualité d’une récréation est relative à la valeur de ses éléments constitutifs : les données, les conditions et l’inconnue. De même, elle est très liée par les éléments de présentation qui sont le titre ou sujet, les illustrations, le texte ou explications.

On peut vérifier

- si toutes les informations contiennent des éléments susceptibles d’être traduits en langage mathématique.

- s’il y a trop de détails, trop de mots superflus, trop de périphrases déroutantes

- si l’emploi du vocabulaire est adéquat

- si les illustrations choisies enrichissent le problème

- si les pièges ont un rôle positif.

Conclusion
Une récréation ne doit pas être réduite à un exercice de compréhension de texte. Il faut distinguer entre le mode de présentation d’une récréation et la récréation elle-même. L’énoncé et les illustrations sont des objets concrets, visibles et fixes ; le problème est un objet abstrait qui change à mesure que progresse la compréhension de l’énoncé. Le problème prend son sens dans la représentation mentale de l’amateur.

La récréation sera donc reçue en deux volets bien distincts :
- la réaction face à l’ensemble du problème tant au point de vue de la forme que du contenu
- la réaction face aux écueils, aux difficultés ou au plaisir de la résolution.

En somme, le choix des récréations repose sur des critères essentiellement personnels. Non seulement la récréation ne doit pas rebuter, mais elle doit porter en elle des points d’accrochage peut-être subtils mais sûrement significatifs. ç

Solutions

Solution 1. Il y a 24 façons d’écrire un nombre ayant quatre chiffres différents. Le groupe est composé de 24 personnes.

Solution 2. Marin possède 429 $.

Solution 3. On peut compter cinq terrains carrés.

Solution 4. Luc rapporte 4 béatitudes et Mathieu 8. Le nombre cherché est 74 642 ou 74 682.

Solution 5. Gaston a 41 ans et Luce 52.

Solution 6. Alcide est l’ancêtre.

Solution 7. Le problème est insoluble.

Solution 8. Les possibilités sont données à la suite du problème.

Solution 9. Voici une façon de placer les nombres :

Solution 10. Le carré obtenu par la différence de deux carrés a deux chiffres, car un mouton a deux oreilles. La différence de carrés est 81, 49, 25 ou 9. On aura donc 41² - 40², 25² - 24², 13² - 12² ou 5² - 4². Comme le nombre cherché a quatre chiffres (un mouton a quatre pattes), Érica compta 41² ou 1 681 moutons.

Solution 11. Les nombres sont 20 et 28.

Solution 12. Martin a parcouru 20 kilomètres et Martine 28.

Solution 13. Pierre a cueilli 20 pommes et Pierrette 28.

Solution 14. Louis a 20 ans et Valérie 28 ans.

Solution 15. Cardio a 20 robots et Vasculo 28.

Solution 16. Deux femmes passent et l’une ramène le bateau ; puis deux femmes passent encore et l’une ramène le bateau et demeure avec son mari. Les deux autres maris passent, puis l’un d’eux avec sa femme retourne au bateau. Les deux hommes passent et la femme repasse ; puis deux femmes passent. Il ne reste plus que l’un des maris qui va quérir sa femme.

Solution 17. Deux dames vont à l’îlot Nelligan. Une dame revient et accompagne la troisième dame. Une dame revient à l’îlot Fréchette et demeure avec son roi. Les deux autres rois passent à l’îlot Nelligan. Un roi revient avec sa dame qu’il laisse et accompagne l’autre roi vers l’îlot Nelligan. La dame qui est seule avec les rois revient à l’îlot Fréchette et accompagne une des autres dames. L’un des rois va chercher sa dame et l’amène à l’îlot Nelligan.

Solution 18. Voici une disposition des nombres :

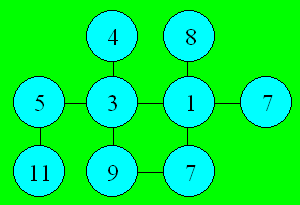
Les deux rangées verticales de trois cercles peuvent être interverties.