|
Depuis des temps immémoriaux, les jeux de hasard et en particulier les dés ont
eu la ferveur des élites et du peuple. On raconte même que certains dieux
antiques consultaient les dés avant d’accorder des faveurs. Ces dés étaient
de matériaux et de formes diverses, comme des cailloux, des coquillages, des
osselets. À cause de son aspect pratique, le dé cubique a très tôt pris la
meilleure place. C’est un cube léger et de petite taille dont les six faces
sont marquées de 1 à 6. L’arrivée des jeux de rôle a contribué à faire
connaître d’autres formes de dés.
1. Lancers
de deux dés
Lorsqu’un jeu exige le lancer simultané de deux dés, on s’intéresse
la plupart du temps à la somme des marques prises deux à deux. Le tableau
ci-après établit les 36 couples possibles et les sommes qui varient de 2 à 12
lorsque l’on lance deux dés cubiques.
|
+ |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Tableau 1
Les données de ce tableau permettent d’établir la
fréquence de chaque somme et la probabilité d’obtenir celle-ci. Par exemple,
la somme 5 apparaît quatre fois sur 36 ou une fois sur 9. La probabilité de
cet événement est de 1 sur 9.
2. Dés normaux
et conormaux
Dans le cadre de cet article, un dé normal est un dé de
forme polyédrique à n faces qui est marqué d’entiers consécutifs
généralement à partir de 1. Une paire de dés normaux est un ensemble de deux
dés normaux. On pourrait associer ce concept aux jumeaux identiques, soit les
vrais jumeaux. Une paire de dés conormaux est un ensemble de deux dés non
normaux et différents entre eux par leurs marques. Les deux dés sont dits
conormaux parce qu’ils sont associés à une paire de dés normaux si bien que
leurs sommes, la fréquence de chaque somme et la courbe de probabilités sont
les mêmes dans les deux classes de dés. On pourrait associer le concept de
dés conormaux aux jumeaux non identiques, soit les faux jumeaux.
Nous allons produire des dés conormaux formés par six
polyèdres dont cinq, sauf le dé décaédrique, sont des polyèdres
platoniciens.
3. Dés tétraédriques ou D4
Un tétraèdre est formé de quatre faces. Un dé normal de cette
forme est ordinairement marqué de 1 à 4. Si on additionne deux à deux les
marques de rang opposé, comme 1 et 4 ou 2 et 3, la somme est 5. Un dé D4
normal peut être représenté ainsi :
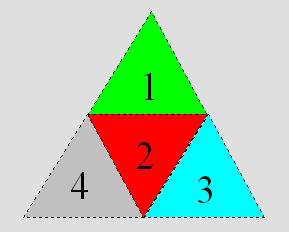
Figure 2
Si on lance simultanément deux de ces dés, la plus petite
somme des couples est 2 et la plus grande 8. La probabilité de chacune de ces
deux sommes est 1/16, car à chaque somme correspond un seul couple, soit (1, 1)
ou (4, 4), sur un total de 16 couples. Voici un tableau qui établit les
couples, leur fréquence et la probabilité en regard de chaque somme :
|
Somme |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Couples |
(1,1) |
(1,2), (2,1) |
(1,3), (2,2), (3,1) |
(1,4), (2,3), (3,2), (4,1) |
(2,4),
(3,3), (4,2) |
(3,4), (4,3) |
(4,4) |
|
Fréquence |
1 |
2 |
3 |
4 |
3 |
2 |
1 |
|
Probabilité |
1/16 |
1/8 |
3/16 |
1/4 |
3/16 |
1/8 |
1/16 |
Tableau 3
À une paire de dés normaux de cette forme, on peut associer
une paire de dés conormaux. Voici comment on peut y arriver :
Pour avoir une somme de 2, il faut qu’une marque de chaque
dé soit 1. Pour avoir deux sommes de 3, il faut ajouter deux 2 sur un dé ou un
2 sur chaque dé. Cette dernière action conduira à des dés normaux. Sur le
premier dé, les marques sont 1, 2, 2 et sur le second 1. Comme dans le dé
normal, la somme des marques de rang opposé est toujours la même, cette
propriété doit être appliquée aux dés conormaux. La somme de 2 et de 2
étant 4, il manque 3 au premier dé pour le rendre symétrique avec le 1. On
écrit, par exemple, 1, 2, 2, 3 en abscisse comme dans le tableau ci-après et
en ordonnée 1. On fait les additions appropriées. On obtient les sommes 2, 3,
3, 4. Sur le second dé, on ne peut pas inscrire 2 car il y aurait trois sommes
3. Comme il manque deux sommes 4, on inscrit deux 3 sur le second dé. On fait
les additions appropriées. La somme 5 apparaît quatre fois comme il se doit.
La somme 6 apparaît deux fois. Comme il manque un 6, on complète le second dé
avec une marque 5, ce qui confirme la symétrie avec le 1. Les dés sont
marqués respectivement 1, 2, 2, 3 et 1, 3, 3, 5. Voici le tableau
complet :
| |
1 |
2 |
2 |
3 |
|
1 |
2 |
3 |
3 |
4 |
|
3 |
4 |
5 |
5 |
6 |
|
3 |
4 |
5 |
5 |
6 |
|
5 |
6 |
7 |
7 |
8 |
Tableau 4
Le tableau suivant établit les couples, leur fréquence et
la probabilité en relation avec chaque somme des deux dés qu’on a
créés.
|
Somme |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Couples |
(1,1) |
(2,1),
(2,1) |
(1,3),
(1,3),
(3,1) |
(2,3),
(2,3),
(2,3),
(2,3) |
(1,5),
(3,3),
(3,3) |
(2,5), (2,5)
|
(3,5) |
|
Fréquence |
1 |
2 |
3 |
4 |
3 |
2 |
1 |
|
Probabilité |
1/16 |
1/8 |
3/16 |
1/4 |
3/16 |
1/8 |
1/16 |
Tableau 5
Si on compare avec le tableau 3, on constate que les sommes,
la fréquence des couples et la probabilité de gain pour chaque somme sont
identiques. Seuls les couples diffèrent. Les deux dés trouvés sont dits
conormaux de deux dés normaux. Voici une représentation :
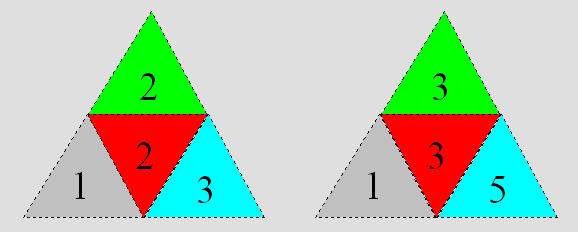
Figure 6
Si on additionne un entier au premier dé et si on soustrait
le même entier au deuxième, on obtient une autre paire de dés conormaux. En
prenant 1 comme entier, on obtient les deux dés de gauche de la figure 7. L’une
des faces d’un dé est 0. En prenant un entier supérieur à 1, on obtient d’autres
paires de dés conormaux. Toutefois, une ou des faces montrent des entiers
négatifs. Un exemple est donné à droite quand on choisit 2.
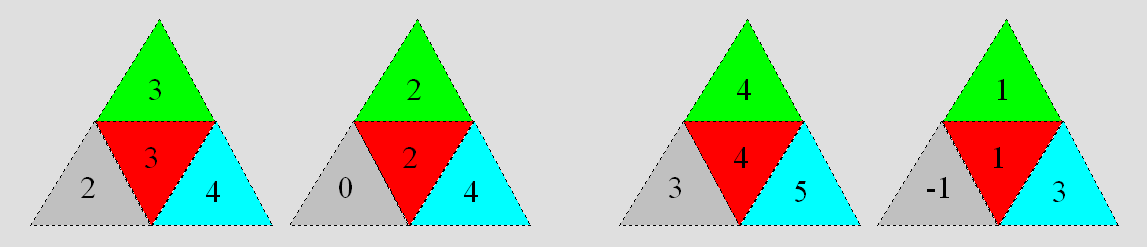
Figure 7
Si on additionne ou soustrait le même entier à une paire de
dés conormaux, on obtient une paire de dés dont les sommes des couples
diffèrent de celles d’une paire de dés normaux. Même si la courbe de
probabilités est identique, ces dés ne sont pas conormaux. Voici un exemple
où on a additionné 2 à chacun des dés de la figure 6 :
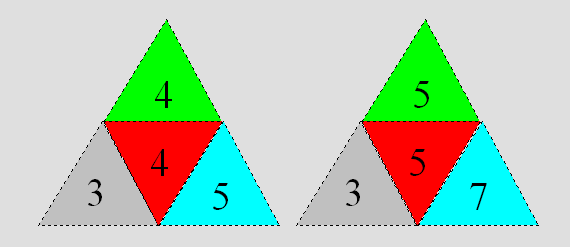
Figure 8
4. Dés hexaédriques ou D6
Un hexaèdre ou cube est formé de six
faces. Un dé normal de cette forme est marqué de 1 à 6. Si on additionne deux
à deux les marques de rang opposé, comme 1 et 6, 2 et 5 ou 3 et 4, la somme
est 7. Un dé D6 normal peut être représenté ainsi :

Figure 9
Si on lance simultanément deux de ces dés, la plus petite
somme des couples est 2 et la plus grande 12. La probabilité de chacune de ces
deux sommes est 1/36, car à chaque somme correspond un seul couple, soit (1, 1)
ou (6, 6), sur un total de 36 couples. Voici un tableau qui établit les
couples, leur fréquence et la probabilité en relation avec chaque somme :
|
Sommes |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Couples |
(1,1) |
(1,2), (2,1) |
(1,3), (2, 2), (3,1) |
(1,4), (2,3), (3,2), (4,1) |
(1,5), (2,4),
(3,3),
(4,2), (5,1) |
(1,6), (2,5), (3,4), (4,3), (5,2)
(6,1) |
(2,6), (3,5),
(4,4), (5,3), (6,2) |
(3,6), (4,5), (5,4), (6,3) |
(4,6), (5, 5), (6,4) |
(5,6), (6,5) |
(6,6) |
|
Fréquence |
1 |
2 |
3 |
4 |
5 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Probabilité |
1/36 |
1/18 |
1/12 |
1/9 |
5/36 |
1/6 |
5/36 |
1/9 |
1/12 |
1/18 |
1/36 |
Tableau 10
À une paire de dés normaux de cette forme, on peut associer
une paire de dés conormaux. Voici comment on peut y arriver :
Pour avoir une somme de 2, il faut qu’une marque de chaque
dé soit 1. Pour avoir deux sommes de 3, il faut ajouter deux 2 sur un dé ou un
2 sur chaque dé. Cette dernière action conduira à deux dés normaux. Sur un
premier dé, on a donc 1, 2, 2. Sur le second dé, on ne peut pas inscrire 2 car
il y aurait trois sommes 3. Pour avoir trois sommes 4, il faut inscrire trois 3
sur les dés. Pour respecter le principe de la symétrie, on place deux 3 sur le
premier dé car les deux marques précédentes, soit 2 et 2, sont identiques. On
inscrit le troisième 3 sur le second dé. On fait les sommes comme dans le
tableau ci-après. La somme des marques symétriques du premier dé est 5. On
complète le premier dé avec un 4. Le premier dé est marqué 1, 2, 2, 3, 3, 4.
La prochaine marque du second dé sera un 4 car il manque une somme 5. On
continue ainsi en complétant au fur et à mesure ce tableau.
| |
1 |
2 |
2 |
3 |
3 |
4 |
|
1 |
2 |
3 |
3 |
4 |
4 |
5 |
|
3 |
4 |
5 |
5 |
6 |
6 |
7 |
|
4 |
5 |
6 |
6 |
7 |
7 |
8 |
|
5 |
6 |
7 |
7 |
8 |
8 |
9 |
|
6 |
7 |
8 |
8 |
9 |
9 |
10 |
|
8 |
9 |
10 |
10 |
11 |
11 |
12 |
Tableau 11
Le second dé est marqué 1, 3, 4, 5, 6, 8. Le tableau
suivant établit les couples, leur fréquence et la probabilité en relation
avec chaque somme des deux dés trouvés.
|
Somme |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Couples |
(1,1) |
(2,1),
(2,1) |
(1,3),
(3,1),
(3,1) |
(1,4),
(2,3),
(2,3),
(4,1) |
(1,5),
(2,4),
(2,4),
(3,3),
(3,3) |
(1,6),
(2,5), (2,5),
(3,4),
(3,4),
(4,3) |
(2,6),
(2,6),
(3,5),
(3,5),
(4,4) |
(1,8),
(3,6),
(3,6),
(4,5) |
(2,8),
(2,8),
(4,6) |
(3,8), (3,8) |
(4,8) |
|
Fréquence |
1 |
2 |
3 |
4 |
5 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Probabilité |
1/36 |
1/18 |
1/12 |
1/9 |
5/36 |
1/6 |
5/36 |
1/9 |
1/12 |
1/18 |
1/36 |
Tableau 12
Si on compare avec le tableau 10, les sommes, la fréquence
des couples et la probabilité de gain pour chaque somme sont identiques. Seuls
les couples diffèrent. Les deux dés trouvés sont dits conormaux de deux dés
normaux. Voici leur représentation :
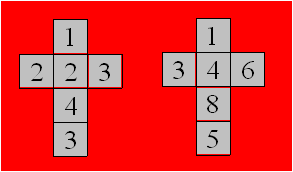
Figure 13
Cette paire de dés qu’on a obtenue a été imaginée par l’Américain
George Sicherman et popularisée par Martin Gardner (1914-2010) en 1978. Il a été
démontré que cette paire est unique dans l’ensemble des entiers naturels.
Dans le premier dé de cette paire, les faces opposées ont une somme de 5 et
dans le second, la somme est 9. Si on additionne les deux sommes, on obtient 14
qui est deux fois la somme des faces opposées d’un dé D6 normal.
On peut additionner un entier à chaque face d’un dé et
soustraire le même entier à chaque face de l’autre dé. Si on additionne 1
au premier dé de la figure 13 et si on soustrait 1 au second dé, obtient les
dés de gauche de la figure ci-après. Si on fait les mêmes opérations dans l’ordre
inverse, on obtient les deux dés de droite. Dans les deux cas, l’un des dés
a une face marquée 0. On a là deux paires de dés conormaux.
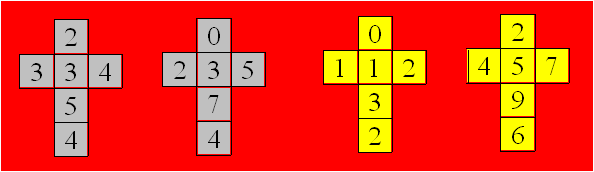
Figure 14
En additionnant 2 et en soustrayant 2 à chacun des deux dés
de Sicherman, on obtient une autre paire de dés conormaux même si l’une des
faces montre un entier négatif. Ceux-ci sont représentés à gauche dans la
figure ci-après. Si on additionne 3 à chacun des deux dés de gauche, les deux
dés ne sont pas conormaux car les sommes varient de 8 à 18 au lieu de 2 à 12.
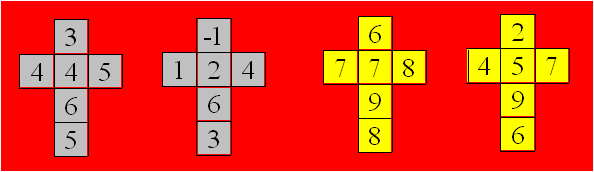
Figure 15
5. Dés octaédriques ou D8
Un octaèdre est formé de huit faces. Un dé normal de cette forme
est ordinairement marqué de 1 à 8. Si on additionne deux à deux les marques
de rang opposé, la somme est 9. Un dé D8 normal peut être représenté
ainsi :
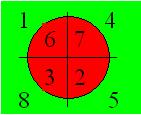
Figure 16
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Tableau 17
En s’inspirant des démarches précédentes, on peut créer
une paire de dés conormaux. Ces dés sont marqués respectivement 1, 2, 2, 3,
3, 4, 4, 5 et 1, 3, 5, 5, 7, 7, 9, 11. Le tableau suivant établit les sommes
pour chaque couple.
| |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
|
1 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
|
3 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
|
5 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
10 |
|
5 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
10 |
|
7 |
8 |
9 |
9 |
10 |
10 |
11 |
11 |
12 |
|
7 |
8 |
9 |
9 |
10 |
10 |
11 |
11 |
12 |
|
9 |
10 |
11 |
11 |
12 |
12 |
13 |
13 |
14 |
|
11 |
12 |
13 |
13 |
14 |
14 |
15 |
15 |
16 |
Tableau 18
En comparant les tableaux 17 et 18, on constate que, dans les
deux cas, les sommes varient de 2 à 16. On peut vérifier que chaque somme a la
même fréquence d’un tableau à l’autre. En conséquence, la probabilité d’obtenir
une somme donnée est identique en regard de chaque somme. Voici une façon de
représenter ces deux dés D8 conormaux :
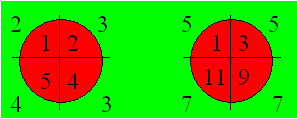
Figure 19
Comme pour les dés des autres formes, on peut faire des
opérations d’addition et de soustraction et obtenir d’autres dés, mais pas
nécessairement conormaux.
6. Dés décaédriques ou D10
Un décaèdre est formé de 10 faces. Un dé normal de cette forme
est ordinairement marqué de 0 à 9. Pour les fins de comparaison avec les
autres dés, on marque le dé décaédrique de 1 à 10. Voici une
représentation de ce dé :
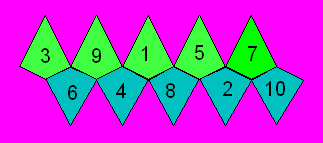
Figure 20
Si on additionne deux à deux les marques de rang opposé,
leur somme est 11. Si on lance simultanément deux dés, la plus petite somme
est 2 et la plus grande 20. En s’inspirant des démarches précédentes, on
peut créer une paire de dés conormaux. Ces dés sont marqués respectivement
1, 2, 2, 3, 3, 4, 4, 5, 5, 6 et 1, 3, 5, 6, 7, 8, 9, 10, 12, 14. Le tableau
suivant établit les sommes pour chaque couple.
|
|
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
|
1 |
2 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
|
3 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
8 |
9 |
|
5 |
6 |
7 |
7 |
8 |
8 |
9 |
9 |
10 |
10 |
11 |
|
6 |
7 |
8 |
8 |
9 |
9 |
10 |
10 |
11 |
11 |
12 |
|
7 |
8 |
9 |
9 |
10 |
10 |
11 |
11 |
12 |
12 |
13 |
|
8 |
9 |
10 |
10 |
11 |
11 |
12 |
12 |
13 |
13 |
14 |
|
9 |
10 |
11 |
11 |
12 |
12 |
13 |
13 |
14 |
14 |
15 |
|
10 |
11 |
12 |
12 |
13 |
13 |
14 |
14 |
15 |
15 |
16 |
|
12 |
13 |
14 |
14 |
15 |
15 |
16 |
16 |
17 |
17 |
18 |
|
14 |
15 |
16 |
16 |
17 |
17 |
18 |
18 |
19 |
19 |
20 |
Tableau 21
Voici une façon de représenter ces deux dés D10
conormaux :
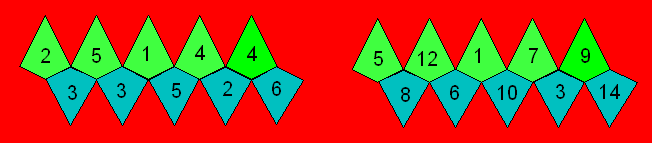
Figure 22
Comme pour les dés des autres formes, on peut faire des
opérations d’addition et de soustraction et obtenir d’autres dés, mais pas
nécessairement conormaux.
7. Dés dodécaédriques ou D12
Un dodécaèdre est formé de 12 faces. Un dé normal de cette forme
est marqué de 1 à 12. Si on additionne deux à deux les marques de rang
opposé, leur somme est 13. Voici une représentation de ce dé :

Figure 23
Si on lance simultanément deux dés, la plus petite somme
est 2 et le plus grande est 24. On peut créer une paire de dés conormaux. Ces
dés sont marqués respectivement 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7 et 1, 3, 5,
7, 7, 9, 9, 11, 11, 13, 15, 17. Voici une façon de représenter cette
paire de dés D12 conormaux :
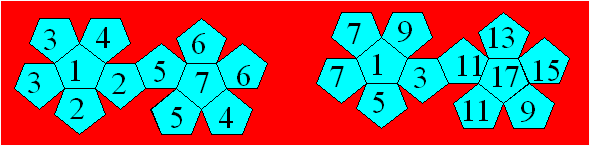
Figure 24
8. Dés icosaédriques ou D20
Un icosaèdre est formé de 20 faces. Un dé normal de cette forme
est marqué de 1 à 20 ou deux fois de 0 à 9. Voici une représentation de
chacun de ces deux dés :
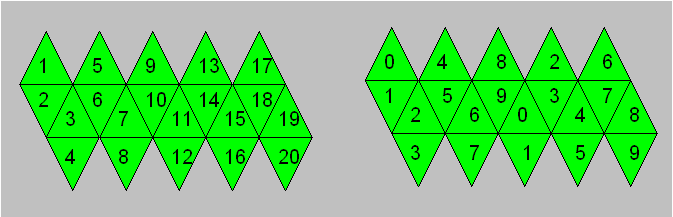
Figure 25
Pour les fins de comparaison avec les autres dés, on
considère seulement le premier dé. Si on additionne deux à deux les marques
de rang opposé, la somme est 21. On peut créer une paire de dés conormaux.
Ces dés sont marqués respectivement 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8,
8, 9, 9, 10, 10, 11 et 1, 3, 5, 7, 9, 11, 11, 13, 13, 15, 15, 17, 17, 19, 19,
21, 23, 25, 27, 29. Voici une façon de représenter ces deux dés D20
conormaux :
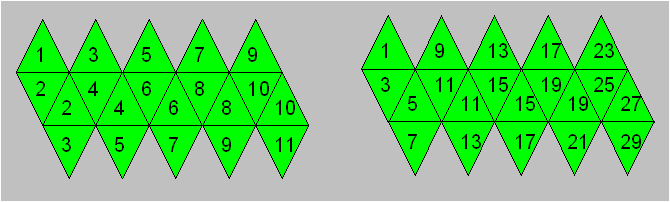
Figure 26
En guise de conclusion
Pour chacun des dés polyédriques étudiés, nous avons produit une
paire de dés conormaux qu’on peut associer à une paire de dés normaux. Pour
l’une ou l’autre paire, si deux joueurs se partagent les sommes, les
probabilités de gains sont exactement les mêmes. Les marques des paires de
dés conormaux sont reprises ici.
Tétraédriques
ou D4 : 1, 2, 2, 3 et 1, 3, 3, 5
Hexaédriques ou
D6 : 1, 2, 2, 3, 3, 4 et 1, 3, 4, 5, 6, 8
Octaédriques ou
D8 : 1, 2, 2, 3, 3, 4, 4, 5 et 1, 3, 5, 5, 7, 7, 9, 11
Décaédriques ou
D10 : 1, 2, 2, 3, 3, 4, 4, 5, 5, 6 et 1, 3, 5, 6, 7, 8, 9, 10, 12, 14
Dodécaédriques ou
D12 : 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7 et 1, 3, 5, 7, 7, 9, 9, 11, 11, 13, 15,
17
Icosaédriques
ou D20 : 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10, 11 et
1, 3, 5, 7, 9, 11, 11, 13, 13, 15, 15, 17, 17, 19, 19, 21, 23, 25, 27, 29
Le tableau suivant donne, pour chaque paire de dés
polyédriques conormaux de n faces, la plus petite somme (PP), la plus
grande somme (PG), la somme des marques opposées du premier dé (C1), la même
somme pour le second dé (C2), la somme des marques du premier dé (S1), la
même somme pour le second dé (S2) et le total (TD) pour le dé.
| |
D4 |
D6 |
D8 |
D10 |
D12 |
D20 |
Formules |
|
n |
4 |
6 |
8 |
10 |
12 |
20 |
|
|
PP |
2 |
2 |
2 |
2 |
2 |
2 |
|
|
PG |
8 |
12 |
16 |
20 |
24 |
40 |
2n |
|
C1 |
4 |
5 |
6 |
7 |
8 |
12 |
(n + 4)/2 |
|
C2 |
6 |
9 |
12 |
15 |
18 |
30 |
3n/2 |
|
S1 |
8 |
15 |
24 |
35 |
48 |
120 |
n (n
+ 4)/4 |
|
S2 |
12 |
27 |
48 |
75 |
108 |
300 |
3n2/4 |
|
TD |
20 |
42 |
72 |
110 |
156 |
420 |
n (n
+ 1) |
Tableau 27
Pour chaque somme, une formule algébrique est donnée en fonction du nombre
de faces des dés. On peut penser qu’au moins une paire de dés conormaux
existe pour chaque forme polyédrique d’ordre n quand n est
pair. Cette paire de dés conormaux pour chaque polyèdre est-elle unique dans l’ensemble
des entiers naturels comme il a été démontré pour la paire de
Sicherman ? C’est là un problème non résolu. Par ailleurs, une paire
de dés conormaux étant trouvée, en appliquant des opérations
simultanées d’addition ou de soustraction avec un même entier, on peut définir une
infinité d’autres dés conormaux pour chaque forme polyédrique. Û
|
|
![]()
![]()