|
La migration des oiseaux est un
phénomène connu. Certaines espèces se déplacent en triangles pour maximiser
leurs énergies. Selon Édouard Lucas (1842-1891), il est probable que
l'observation du vol des oiseaux a amené la création des nombres
triangulaires. Ces nombres sont formés par la sommation des entiers naturels
consécutifs à partir de l'unité. Ainsi, 15 est un nombre triangulaire, car 1
+ 2 + 3 + 4 + 5 = 15. La représentation de ces nombres se fait par des points
ou des petits cercles disposés en un triangle équilatéral. La notation
conventionnelle utilisée pour désigner un nombre triangulaire est Tn
où n est le rang du terme. Par exemple, T5
= 15. Voici sa représentation :
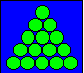
Au lieu d'utiliser la notation
conventionnelle, nous allons introduire un nouveau symbole D
que nous appellerons triangle
et qui devient la puissance triangulaire d'un entier naturel donné. Par
exemple, aD
se lit a élevé à la puissance
triangle ou, plus brièvement, a au triangle. Nous pouvons donc écrire
: 1D
= 1, 2D = 3, 3D
= 6, 4D = 10, 5D
= 15 ... et plus généralement aD
= a(a + 1)/2. Cette nouvelle notation
exprime une puissance au lieu d'indiquer un rang.
Un problème
Dans cet article, nous allons résoudre un problème
concernant des configurations formées par un nombre triangulaire d’oiseaux,
suggérer deux autres situations et discuter de l’aspect didactique du
problème. Toute configuration triangulaire d'oiseaux qui contient pD
oiseaux est formée de p files, une file étant
une rangée horizontale d’oiseaux.
Problème.
Deux
ou plusieurs configurations triangulaires, distinctes ou pas, doivent se
transformer en une configuration triangulaire d’oiseaux. Trouvez une
formule générale qui permet de résoudre l’équation associée.
|
Pour faciliter la démarche, on part de
la configuration triangulaire à laquelle on devrait normalement aboutir et on
la transforme en deux ou plusieurs configurations triangulaires. On commence par
déplacer les oiseaux de la file de la base, puis des files adjacentes en allant
vers le sommet. On conserve ainsi un triangle d’oiseaux au sommet.
Nous allons
étudier successivement les situations où deux, trois, puis quatre
configurations triangulaires d’oiseaux se transforment en une seule
configuration triangulaire. Dans chacun des cas, nous procéderons au
déplacement des oiseaux d’une file, de deux, de trois, puis de q
files. Nous aboutirons ainsi à une formule générale permettant de résoudre
l’équation associée.
1.0
Passage de deux configurations triangulaires d’oiseaux à une seule
Problème
auxiliaire. Deux configurations triangulaires d’oiseaux doivent se
transformer en une configuration triangulaire. Trouvez une formule qui
permet de résoudre l’équation associée.
|
Cela revient
à résoudre une équation de la forme aD
+ bD = cD.
Recherchons les solutions de l’équation en considérant
que les oiseaux de la file ou des files de la base se déplacent à partir de
la configuration unique.
1.1 Déplacement d’une file d’oiseaux
Une configuration triangulaire qui permet le
déplacement d’une file d’oiseaux de la base est 10D
= 55. Les 10 oiseaux de la base se déplacent et forment un
triangle de quatre files. Les neuf autres files restent en place. En voici l’illustration :
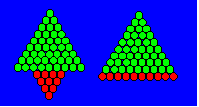
Cette figure illustre l’identité :
4D
+ 9D = 10D.
En d’autres mots, a = 4, b = 9 et c
= 10. Voici d’autres solutions de l’équation :
|
a |
2 |
3 |
5 |
6 |
7 |
8 |
|
b |
2 |
5 |
14 |
20 |
27 |
35 |
|
c |
3 |
6 |
15 |
21 |
28 |
36 |
Cela donne les
identités suivantes : 2D
+ 2D = 3D,
3D + 5D
= 6D, 5D
+ 14D = 15D,
etc. Pour trouver une solution de l’équation aD
+ bD = cD,
quand on déplace une file, on donne à a une
valeur entière autre que l’unité. Alors, b = aD
-
1 et c = b + 1. Notons que, dans
ce cas, c est aussi un triangulaire.
1.2 Déplacement de deux files d’oiseaux
Une configuration triangulaire qui permet le
déplacement de deux files d’oiseaux de la base est 11D
= 66. Les neuf files du sommet restent en place et les deux
de la base contenant 21 oiseaux forment un triangle de six files. En voici l’illustration :
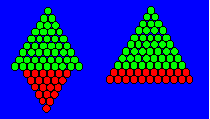
Cette figure illustre l’identité :
6D
+ 9D = 11D.
En d’autres mots, a = 6, b = 9
et c = 11. Voici d’autres solutions de l’équation :
|
a |
5 |
9 |
10 |
13 |
14 |
17 |
|
b |
6 |
21 |
26 |
44 |
51 |
75 |
|
c |
8 |
23 |
28 |
46 |
53 |
77 |
Cela donne les
identités suivantes : 5D
+ 6D = 8D,
9D + 21D
= 23D, etc.
Pour trouver une solution de l’équation aD
+
bD
= cD, quand
on déplace deux files, on donne à a une valeur entière telle que
aD est impair. Alors, b
= (aD - 3)/2 et c =
b + 2.
1.3 Déplacement de trois files d’oiseaux
Une configuration triangulaire qui permet le
déplacement de trois files d’oiseaux de la base est 8D
= 36. Les cinq files du sommet restent en place et les
trois de la base contenant 21 oiseaux forment un triangle de cinq files. En
voici l’illustration :
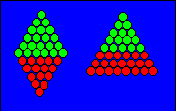
Cette figure illustre l'identité : 6D
+ 5D = 8D.
Voici d’autres solutions de l’équation :
|
a |
5 |
8 |
9 |
11 |
12 |
14 |
|
b |
3 |
10 |
13 |
20 |
24 |
33 |
|
c |
6 |
13 |
16 |
23 |
27 |
36 |
Cela donne les
identités suivantes : 5D
+ 3D = 6D,
8D + 10D
= 13D, etc.
Pour trouver une solution de l’équation aD
+ bD = cD,
quand on déplace trois files, on donne à a une
valeur entière telle que aD est
un multiple de 3. Alors, b = (aD -
6)/3 et c = b + 3.
1.4 Déplacement de q files d’oiseaux
Pour proposer une solution de l’équation aD
+ bD = cD,
quand on déplace q files, on compare les
résultats obtenus.
Pour
le déplacement d’une file : b = aD -
1 et c = b + 1
Pour
le déplacement de deux files : b
= (aD - 3)/2 et c
= b + 2.
Pour
le déplacement de trois files : b
= (aD - 6)/3 et
c = b + 3.
On constate
que la valeur de b est la différence de aD
et de qD qu’on
divise par q. La valeur de c est la somme de b et de q.
Aussi, on donne à a une valeur entière telle que (aD
- qD) est
un multiple de q. Alors, b = (aD
- qD)/q et c
= b + q.
2.0 Passage
de trois configurations triangulaires d’oiseaux à une seule
Problème auxiliaire. Trois
configurations triangulaires d’oiseaux doivent se transformer en une
configuration triangulaire. Trouvez une formule qui permet de résoudre l’équation
associée.
|
Cela revient
à résoudre l'équation de la forme aD
+ bD + cD
= dD . Recherchons
les solutions en considérant que les oiseaux de la file ou des files de la base
se déplacent à partir de la configuration unique.
2.1 Déplacement d’une file d’oiseaux
Une configuration triangulaire qui permet le
déplacement d’une file d’oiseaux de la base est 9D
= 45. Les huit files du sommet restent en place et celle de
la base contenant neuf oiseaux forme deux triangles : l’un de trois et l’autre
de six oiseaux. En voici l’illustration :
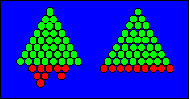
Cette figure illustre l’identité :
2D
+ 3D + 8D
= 9D. Voici
d’autres solutions de l’équation :
|
a |
2 |
2 |
2 |
2 |
2 |
3 |
|
b |
2 |
4 |
5 |
6 |
7 |
5 |
|
c |
5 |
12 |
17 |
23 |
30 |
20 |
|
d |
6 |
13 |
18 |
24 |
31 |
21 |
Pour trouver
une solution de l’équation aD
+ bD + cD
= dD, quand
on déplace une file, on donne à a et à b toute valeur
entière autre que l’unité. Alors, c = aD
+ bD - 1 et d
= c + 1.
2.2 Déplacement de deux files d’oiseaux
Une configuration triangulaire qui permet le
déplacement de deux files d’oiseaux de la base est 7D
= 28. Les cinq files du sommet restent en place et les deux
de la base contenant 13 oiseaux forment deux triangles : l’un de trois oiseaux
et l’autre de 10 oiseaux. En voici l’illustration :
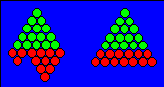
Cette figure illustre l’identité :
2D
+ 4D + 5D
= 7D . Voici
d’autres solutions de l’équation :
|
a |
2 |
2 |
3 |
3 |
3 |
4 |
|
b |
7 |
8 |
5 |
6 |
9 |
5 |
|
c |
14 |
18 |
9 |
12 |
24 |
11 |
|
d |
16 |
20 |
11 |
14 |
26 |
13 |
Pour trouver
une solution de l’équation aD
+ bD + cD
=
dD, quand
on déplace deux files, on donne à a et à b des valeurs
entières telles que (aD
+ bD)
est impaire. Alors, c
= (aD + bD
- 3)/2 et d = c + 2.
2.3 Déplacement de trois files d’oiseaux
Une configuration triangulaire qui permet le
déplacement de trois files d’oiseaux de la base est 10D
= 55. Les sept files du sommet restent en place et les
trois de la base contenant 27 oiseaux forment deux triangles : l’un de six et
l’autre de 21 oiseaux. En voici l’illustration :

Cette figure illustre l’identité :
3D
+ 6D + 7D
= 10D. Voici
d’autres solutions de l’équation :
|
a |
2 |
2 |
2 |
3 |
3 |
5 |
|
b |
8 |
9 |
9 |
3 |
8 |
6 |
|
c |
11 |
14 |
15 |
2 |
12 |
10 |
|
d |
14 |
17 |
18 |
5 |
15 |
13 |
Pour trouver
une solution de l’équation aD
+ bD + cD
= dD, quand
on déplace trois files, on donne à a et à b des valeurs
entières telles que (aD + bD
) est un multiple de 3. Alors, c = (aD
+ bD - 6)/3 et d = c
+ 3.
2.4 Déplacement de q files d’oiseaux
Pour trouver une solution de l’équation aD
+ bD + cD
= dD, quand
on déplace q files, on compare d’abord les résultats obtenus.
Pour
le déplacement d’une file : c = aD +
bD - 1 et d =
c + 1.
Pour
le déplacement de deux files : c = (aD + bD
- 3)/2 et d = c + 2.
Pour
le déplacement de trois files : c
= (aD + bD
- 6)/3 et d = c + 3.
On constate
que la valeur de c est la différence de (aD
+ bD)
et de qD
qu’on divise par q. La valeur de d est
la somme de c
et de q. Aussi, on donne à a et à b des valeurs
entières telles que (aD + bD
- qD)
est un multiple de q. Alors, c = (aD
+ bD - qD)/q
et d = c + q.
3.0 Passage
de quatre configurations triangulaires
d’oiseaux à une seule
Problème auxiliaire. Quatre
configurations triangulaires se transforment en une configuration
triangulaire. Trouvez une formule qui permet de résoudre l’équation
associée.
|
Cela revient
à résoudre l'équation aD
+ bD + cD
+ dD = eD.
Recherchons les solutions en considérant que les oiseaux
de la file ou des files de base se déplacent à partir d’une configuration
unique.
3.1 Déplacement d’une file d’oiseaux
Une configuration triangulaire qui permet le
déplacement d’une file d’oiseaux de la base est 12D
= 78. Les 11 files du sommet restent en place et celle de
la base contenant 12 oiseaux forme trois triangles : deux de trois oiseaux et un
autre de six. En voici l’illustration :

Cette figure illustre l’identité :
2D
+ 2D + 3D
+ 11D = 12D.
Voici d’autres solutions de l’équation :
|
a |
2 |
2 |
2 |
2 |
2 |
3 |
|
b |
2 |
2 |
3 |
3 |
3 |
3 |
|
c |
2 |
4 |
3 |
4 |
5 |
3 |
|
d |
8 |
15 |
14 |
18 |
23 |
17 |
|
e |
9 |
16 |
15 |
19 |
24 |
18 |
Pour trouver
une solution de l’équation aD
+ bD + cD
+ dD = eD,
quand on déplace une file, on donne à a, à b
et à c
toute valeur entière autre que l’unité. Alors, d = aD
+ bD + cD
- 1 et e = d + 1.
3.2 Déplacement de deux files d’oiseaux
Une configuration triangulaire qui permet le
déplacement de deux files d’oiseaux de la base est 10D
= 55. Les huit files du sommet restent en place et les deux
de la base contenant 19 oiseaux forment trois triangles respectivement de 3, 6
et 10 oiseaux. En voici l’illustration :
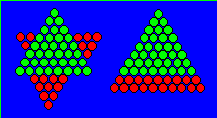
Cette figure illustre l’identité :
2D
+ 3D + 4D
+ 8D = 10D.
Voici d’autres solutions de l’équation :
|
a |
2 |
2 |
2 |
3 |
3 |
4 |
|
b |
2 |
2 |
2 |
3 |
4 |
4 |
|
c |
2 |
5 |
6 |
5 |
5 |
5 |
|
d |
3 |
9 |
12 |
12 |
14 |
16 |
|
e |
5 |
11 |
14 |
14 |
16 |
18 |
Pour trouver
une solution de l’équation aD
+ bD + cD
+ dD = eD,
quand on déplace deux files, on donne à a, à b
et à c
des valeurs entières telles que (aD+
bD + cD)
est impair. Alors, d = (aD
+ bD + cD
- 3)/2 et e = d + 2.
3.3 Déplacement de trois files d’oiseaux
Une configuration triangulaire qui permet le
déplacement de trois files d’oiseaux de la base est 11D
= 66. Les huit files du sommet restent en place et les
trois de la base contenant 30 oiseaux forment trois triangles de 10 oiseaux
chacun. En voici l’illustration :
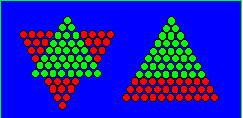
Cette figure illustre l’identité :
4D
+ 4D + 4D
+ 8D = 11D.
Voici d’autres solutions de l’équation :
|
a |
2 |
2 |
2 |
2 |
3 |
3 |
|
b |
2 |
2 |
2 |
3 |
3 |
3 |
|
c |
3 |
5 |
6 |
3 |
3 |
5 |
|
d |
2 |
5 |
7 |
3 |
4 |
7 |
|
e |
5 |
8 |
10 |
6 |
7 |
10 |
Pour trouver
une solution de l’équation aD
+ bD + cD
+ dD = eD
quand on déplace trois files, on donne à a, à b
et à c
des valeurs entières telles que aD
+ bD + cD
est un multiple de 3. Alors, d = (aD
+ bD + cD
- 6)/3 et e = d + 3.
3.4 Déplacement de q files d’oiseaux
Pour trouver une solution de l’équation aD
+ bD + cD
+ dD = eD,
quand on déplace q files, on compare d’abord les
résultats obtenus.
Pour
le déplacement d’une file : d = aD +
bD + cD
- 1 et e = d + 1.
Pour
le déplacement de deux files : d = (aD + bD
+ cD - 3)/2 et e
= d + 2.
Pour
le déplacement de trois files : d
= (aD + bD
+ cD - 6)/3 et e
= d + 3.
On constate
que la valeur de c est la différence de (aD
+ bD + cD
) et de qD qu’on
divise par q. La valeur de e est la somme de d et de q.
Aussi, on donne à a, à b et à c des valeurs entières
telles que (aD + bD
+ cD - qD)
est un multiple de q. Alors, d = (aD
+ bD + cD
- qD)/q et e
= d + q.
4.0 Passage
de p configurations triangulaires à une seule
Pour trouver une solution de l’équation aD
+ bD + cD
+ dD + ... + mD
= nD, quand
on déplace q files, on compare d’abord les résultats obtenus.
Pour
le passage de deux configurations à une seule : b = (aD
- qD)/q et c
= b + q.
Pour
le passage de trois configurations à une seule : c = (aD + bD
- qD)/q et d
= c + q.
Pour
le passage de quatre configurations à une seule : d =
(aD
+ bD + cD
- qD)/q et e
= d + q.
Seules les deux dernières variables ont
besoin d’être calculées. Aux autres qui leur sont antérieures, on donne une
valeur arbitraire. L’avant-dernière variable est la différence de aD
ou de (aD + bD
+ ... ) et de qD qu’on
divise par q. La valeur de la dernière variable est la somme de l’avant-dernière
et de q. Des solutions existent lorsque (aD
+ bD + cD
+ dD + ... - qD)
est un multiple de q. Alors, m = (aD
+ bD + cD
+ dD + ... - qD)/q
et n = m + q.
Procédons à un exemple : Soit à
résoudre l’équation :
aD + bD
+ cD + dD
+ eD = fD.
Si une file d’oiseaux se déplace, q
= 1. Alors, e = aD
+ bD + cD
+ dD - 1 et f
= e + 1. Toute valeur peut être donnée
aux quatre premières variables. Par exemple, si a = 2, b = 3, c
= 4 et d
= 5, alors, e = 2D
+ 3D
+ 4D + 5D
- 1 = 33 et f = 33 + 1 = 34. On peut
écrire : 2D
+ 3D + 4D
+ 5D + 33D
= 34D.
Si deux files d’oiseaux se
déplacent, q = 2. Alors, e = (aD
+ bD + cD
+ dD - 3)/2 et f
= e + 2. La somme des quatre premières
variables doit être impaire. Par exemple, si a = 2, b =
3, c = 4 et d
= 7, alors, e = ( 2D
+ 3D
+ 4D + 7D
- 3)/2 = 22 et f = 22 + 2 = 24. On peut
écrire : 2D
+ 3D + 4D
+ 7D + 22D
= 24D.
Si trois files d’oiseaux se
déplacent, q = 3. Alors, e = (aD
+ bD + cD
+ dD - 6)/3 et f
= e + 3. La somme des quatre premières
variables doit être un multiple de 3. Par exemple, si a = 2, b =
3, c = 5 et d
= 8, alors, e = (2D
+ 3D
+ 5D + 8D
- 6)/3 = 18 et f = 18 + 3
= 21. On peut écrire : 2D +
3D +
5D + 8D
+ 18D =
21D .
Si quatre files d’oiseaux se
déplacent, q = 4. Alors, e = (aD
+ bD + cD
+ dD - 10)/4 et
f = e + 4. La somme des quatre
premières variables doit être un nombre pair qui n’est pas un multiple de 3.
Par exemple, si a
= 2, b = 3, c = 4 et d = 5, alors, e = (2D
+ 3D + 4D
+ 5D - 10)/4 = 6 et f =
6 + 4 = 10. On peut écrire : 2D
+ 3D
+ 4D + 5D
+ 6D = 10D.
Nous
possédons maintenant les outils nécessaires pour connaître le nombre d’oiseaux
requis pour passer de plusieurs configurations à une seule ou encore d’une
seule à plusieurs.
5.0 Deux
autres problèmes
Appliquez les connaissances acquises en résolvant ces
deux problèmes.
5.1 Deux configurations triangulaires d’oiseaux se posent sur le sol pour se
reposer. À leur départ, deux autres configurations doivent être formées.
5.2 Deux configurations triangulaires d’oiseaux
se posent sur le sol et doivent se placer en un carré.
Dans chaque
cas, trouvez une formule générale qui permettrait de fournir toutes les
solutions.
6.0
Aspect didactique
Cette petite aventure avec les oiseaux nous a permis de
voir combien peut être vaste le champ de la recherche mathématique
élémentaire. Nous pourrions, en effet, nous poser bien d’autres questions
sur ce thème.
De plus, cette aventure nous a permis de
vivre la découverte de formules par le raisonnement inductif. En effet, le
raisonnement inductif est une stratégie fort puissante pour la résolution de
problèmes quand les outils n’ont pas encore été développés. Également,
cela nous fait penser qu’il est encore possible d’inventer des symboles ou
des concepts mathématiques pour se faire plaisir.
Cette classe de problèmes peut être
abordée à tous les degrés scolaires : primaire, secondaire, collégial
et universitaire. Les problèmes devraient être énoncés en tenant compte de
la compétence et des connaissances de l’élève. Ils pourraient être
convertis en des problèmes plus simples et des suggestions de démarche
pourraient accompagner les énoncés.
Il est certain que, dans la démarche de
résolution, le symbole D devrait
être adopté seulement quand l’élève a une maîtrise suffisante de l’algèbre.
D’ailleurs, on aurait pu faire tout le travail de recherche sans le symbole D,
puisque, en fin de compte, (aD
+ bD)
exprime la somme de deux nombres triangulaires.
Toutefois, cela nous montre l’importance de la notation symbolique qui permet
de condenser les textes en des formules.
Une autre retombée pédagogique
importante se situe au plan affectif. Pour développer la passion et la
curiosité envers les mathématiques, il faut placer l’élève dans des
conditions où cette science lui apparaîtra comme vivante et pouvant encore
être développée.
Ce type de problèmes est associé aux
mathématiques récréatives, en particulier, à cause de son contenu. Mais
aussi, l’aspect récréatif peut être présent dans la démarche de
résolution. Toutefois, si nous demandions à l’élève de résoudre un
problème spécifique à ce type et si l’élève connaissait la formule, l’aspect
récréatif s’évanouirait. C’est là le paradoxe des mathématiques
récréatives. Elles sont très souvent récréatives quand on est en train de
les construire. Û
________
Références sur les nombres triangulaires
Beiler, Albert H. Recreations in the Theory of Numbers.
New York, Dover, 1964.
Bowers,
H. & Bowers, J. Arithmetical Excursions. New York, Dover, 1961.
Fourrey,
E. Récréations arithmétiques. Paris, Vuibert, 1947.
Gardner,
Martin. Nouveaux divertissements mathématiques. Paris, Dunod, 1970.
Kordemsky,
Boris. The Moscow Puzzles. New York, Scribners, 1972.
Lucas,
Édouard. Théorie des nombres. Paris, Blanchard, 1958.
Lucas,
Édouard. Récréations mathématiques, tome 4. Paris, Blanchard, 1960.
Reichman,
W. J. La fascination des nombres. Paris, Payot, 1959.
Note. Dans la première version
de cet article, nous avions adopté une variable à indices, par exemple a1, a2,
a3, au lieu de a, b, c. Cette version
actuelle est plus facile à lire.
|
![]()
![]()