|
Série A
Solution 34
Les 10 nombres
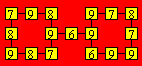
sont : 699, 789, 798, 879, 888, 897, 969, 978, 987 et 996. On peut remplir
chacun des deux carrés et, par la suite, les relier ensemble. Comme il y a
seulement deux nombres qui commencent par 7, on les place dans un coin. Voici
une disposition où seul 888 est omis :
Retour
au problème
|
Un
nombre est divisible par 4 si le nombre formé par ses deux derniers
chiffres est divisible par 4.
|
|
Série
B
Solution 34
Soit
A2 le nombre de campeuses par carré à l’ouverture de la
compétition et B2 le nombre de campeuses par carré dans la salle à
la remise des méritas. On peut écrire : 4A2 - 7B2 =
21. Comme 7B2 et 21 sont des multiples de 7, 4A2 doit
être aussi un multiple de 7. On essaie un carré 7 ´
7 : ce qui donnerait 4 ´ 49 = 196 campeuses. On
fait : 196 - 21 = 175 et 175 ¸ 7 = 25. Comme 25
est un carré, on retient l’hypothèse.
Il y a 196 campeuses dans ce camp.
Retour
au problème
|
Solution
de l’énigme
ALOUETTE
|
|
Série
C
Solution 34
Les
deux derniers chiffres de 41, 42, 43, etc. sont
successivement 04, 16, 64, 56, 24, 96, 84, 36, 44, 76, 04, 16, 64, etc. Il y a
10 nombres différents à partir de 04 jusqu’à 76. On exclut 4 et 16, car ils
sont plus petits que 24.
La
reine a huit colliers.
Retour
au problème
|
Quand
on lance deux dés, on a une chance sur 36 d’avoir un total de deux
points.
|
![]()
![]()