Série A

25. Somme de Mathieu

Dans une grille 6 × 6, Mathieu écrit des nombres. Il prend soin de placer une majorité de groupes de deux nombres dont la somme est 997, ce qui permettra de trouver un nombre-clef.

Encerclez deux par deux les nombres dont la somme est 997. Additionnez les nombres qui restent et vous obtenez le nombre-clef.

Solution

Quelqu’un a l’esprit critique s’il n’accepte aucune assertion sans s’interroger sur sa valeur et s’il tient une proposition pour vraie seulement quand elle a été établie.

25. Pentagone de France

France découpe cinq jetons et les numérote de 1 à 5. Elle place les jetons sur le pentagone aux positions données.

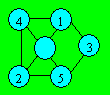
Déplacez les jetons pour que les numéros de 1 à 5 se suivent dans l’ordre sur le contour du pentagone.

Solution

La différence des carrés de deux nombres consécutifs est égale au double du grand nombre auquel on soustrait 1.

Mégane vend des fruits sur le bord du chemin. Le premier jour, elle termine avec un ducat de profit, le deuxième trois ducats, le troisième cinq ducats et ainsi de suite en augmentant le profit de deux ducats par jour. 

Après 20 jours, quel est le profit moyen de Mégane ?  

Le profit moyen est le nombre du ducats gagnés divisé par le nombre de jours.

Solution

© Charles-É. Jean

La somme de deux multiples consécutifs de 5 est 85. Quelle est leur différence ? 

Solution