° Triangle absolu. – Treillis de nombres disposés en un triangle de telle manière que la différence en valeur absolue entre deux nombres voisins sur une même ligne apparaît au milieu de ces deux nombres sur la ligne supérieure. L'ordre du triangle absolu est déterminé par le nombre d'éléments sur la base du triangle. On a trouvé 11 triangles absolus composés d'entiers consécutifs à partir de l'unité : deux d'ordre 2, quatre d'ordre 3, quatre d'ordre 4 et un d'ordre 5. 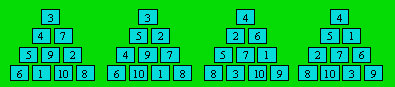Voici les quatre triangles absolus d'ordre 4 :

L’unique triangle absolu d’ordre 5 a été découvert par l’américain George Sicherman. Le voici ci-dessous à gauche :

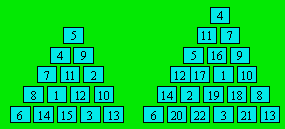
On pense qu'il n'y a pas de triangle absolu d'ordre supérieur à 5 avec des entiers consécutifs à partir de l'unité. Harry L. Nelson a trouvé un triangle d’ordre 6 constitué des entiers de 1 à 22, sauf 15. Il est montré ci-haut à droite. Le Français Damien Guichard a trouvé notamment un triangle d’ordre 7 montré à gauche ci-dessous et contenant 28 nombres de 1 à 33, sauf 7, 20, 21, 24 et 26. Il a aussi trouvé un triangle d’ordre 8 à droite et contenant 36 nombres de 1 à 44, sauf 12, 20, 21, 25, 27, 31, 32 et 35.

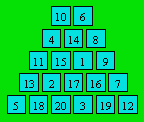
Damien Guichard a proposé d’élargir la définition de triangle absolu. Il considère des triangles tronqués au sommet. Il a donné l’exemple suivant dans lequel un triangle contient tous les entiers de 1 à 20.

Le triangle absolu est associé aux récréations combinatoires.

© Charles-É. Jean

Index : A