Arithmo-géométrique

° Méthode arithmo-géométrique. – Procédé de résolution de problèmes qui consiste à appliquer la géométrie au calcul. Voici un exemple de graphique qui permet de résoudre le problème : Combien y a-t-il de lapins et de poules dans un enclos si on sait qu'il y a en tout 38 têtes et 98 pattes ?

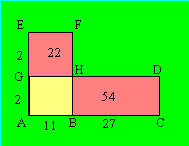
La mesure du segment AB désigne le nombre de lapins, celle du segment BC le nombre de poules, celle du segment AG le nombre de pattes d'une poule et celle du segment AE le nombre de pattes d'un lapin. Le nombre total de pattes, soit 98, correspond à la somme des aires des trois rectangles. On retranche de 98 l'aire du rectangle ACDG, qui est égale à 2 × 38 = 76 : ce qui donne 98 - 76 = 22 pour l'aire du rectangle GHFE. En divisant 22 par 2, on obtient le nombre de lapins, soit 11. Le nombre de poules est 38 - 11 = 27.

© Charles-É. Jean

Index : A