° Graphe gracieux. – Nom donné par l'américain Solomon W. Golomb (1932- ) à un graphe dans lequel chaque paire de sommets est jointe par une arête. Ce graphe, comme un réseau, peut être valué. 

Les sommets doivent recevoir des entiers naturels différents de telle manière qu'ayant fait la différence entre les nombres des deux sommets de chaque arête on obtienne pour les arêtes des entiers naturels consécutifs à partir de l'unité. Les deux premiers graphes ci-dessous sont composés de six arêtes qui sont numérotées de 1 à 6. Les arêtes du troisième graphe reçoivent les nombres de 1 à 11, sauf 6.

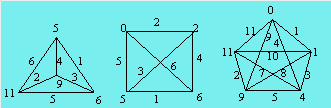
Le troisième graphe n'est pas considéré comme gracieux.

© Charles-É. Jean

Index : G