° Ruban de Möbius. – Figure créée par le mathématicien allemand Möbius en 1839 et formée par une bande de papier qui n'a qu'un seul côté et qu'une seule face. Il s'agit de pratiquer une demi-torsion sur une bande de papier et de coller les extrémités de façon à former un anneau. Cette figure n'a ni envers ni endroit. Un mobile astreint à demeurer sur celui-ci pourrait parcourir sa surface indéfiniment. 

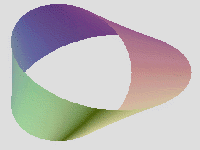
Si on voulait peindre le ruban à partir d'un point, on pourrait le colorier entièrement sans changer de face. Il faut six couleurs pour colorier un ruban de Möbius de telle manière que deux régions voisines d’une carte n'aient jamais la même couleur. 

Le nombre chromatique du ruban de Möbius est donc 6. Son nombre de Betti est 1. 

Si on coupe cette bande le long de sa ligne médiane, on obtient un anneau tordu à deux faces. Si on coupe ce dernier anneau le long de sa ligne médiane, on obtient deux anneaux distincts mais entrelacés. 

Le bonnet croisé et le ruban de Tuckerman sont des formes du ruban de Möbius obtenues après pliage. 

(Image de Futura-Sciences.com)

© Charles-É. Jean

Index : M