|
Segment
Portion de ligne limitée aux deux extrémités. Si la ligne est
droite, on parle de segment de droite, et si elle est courbe, de segment de
courbe. La
construction de figures géométriques avec un nombre déterminé de segments,
tous congruents ou non, peut être l’objet de récréations.
Voici, par
exemple, deux façons de construire quatre triangles et deux carrés avec huit
segments répartis en deux ensembles de quatre segments congruents :
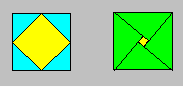
Des segments peuvent représenter tout objet filiforme comme
des crayons, des cure-dents, des allumettes, des clous, des aiguilles, etc.
Voici un carré 2 ´ 2 formé de crayons :
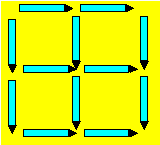
On a besoin de 12 crayons pour former ce carré. On peut s’intéresser
à des rectangles de crayons selon la différence d entre les mesures
entières des côtés du rectangle.
n d = 0. Voici le
nombre de crayons nécessaires pour former des carrés de grandeur donnée
lorsque d = 0.
|
Carré |
1 ´ 1 |
2 ´ 2 |
3 ´ 3 |
4 ´ 4 |
5 ´ 5 |
6 ´ 6 |
7 ´ 7 |
8 ´ 8 |
|
Crayons |
4 |
12 |
24 |
40 |
60 |
84 |
112 |
144 |
Le terme général de rang n de cette suite est 2n(n
+ 1). La différence absolue d’un nombre à un autre est 8, 12, 16, 20, 24,
... soit une suite du premier degré dont la raison est 4.
n d = 1. On a le
tableau suivant.
|
Carré |
1 ´ 2 |
2 ´ 3 |
3 ´ 4 |
4 ´ 5 |
5 ´ 6 |
6 ´ 7 |
7 ´ 8 |
8 ´ 9 |
|
Crayons |
7 |
17 |
31 |
49 |
71 |
97 |
127 |
161 |
Le terme général de rang n de cette suite est 2n2
+ 4n + 1.
n d = 2. On a le
tableau suivant.
|
Carré |
1 ´ 3 |
2 ´ 4 |
3 ´ 5 |
4 ´ 6 |
5 ´ 7 |
6 ´ 8 |
7 ´ 9 |
8 ´ 10 |
|
Crayons |
10 |
22 |
38 |
58 |
82 |
110 |
142 |
178 |
Le terme général de rang n de cette suite est 2(n2
+ 3n + 1).
© Charles-É. Jean
Index
: S
|
![]()
![]()