|
Sierpinski Waclaw (1882-1969)
°
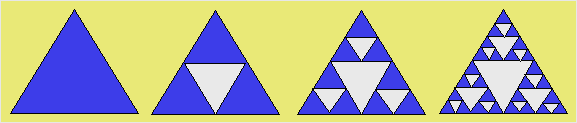
Triangle de Sierpinski.
– Objet fractal réalisé par Sierpinski à partir d'un triangle
équilatéral. Le triangle est d'abord partagé en quatre triangles congruents
dont celui du centre est blanc. Chaque nouveau triangle de couleur est partagé
selon la même règle d'une façon indéfinie. Le résultat final a un
périmètre fini et une aire nulle.
Voici les premières transformations :
Le tableau ci-après donne le nombre de triangles colorés et blancs en
fonction du rang n de la figure.
|
Rang n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
D colorés |
1 |
3 |
9 |
27 |
81 |
243 |
729 |
2187 |
|
D blancs |
0 |
1 |
4 |
13 |
40 |
121 |
364 |
1093 |
|
Total |
1 |
4 |
13 |
40 |
121 |
364 |
1093 |
3280 |
Le nombre de triangles blancs est le total des triangles de
la figure précédente. De façon générale, le nombre de triangles colorés
est 3n-1, le nombre de triangles blancs est (3n-1
- 1)/2 et le total des triangles (3n - 1)/2. Connaissant le
total T des triangles pour une figure de rang n, pour trouver le total
des triangles de la figure de rang (n + 1), on fait (3T + 1).
© Charles-É. Jean
Index
: S
|
![]()
![]()