Dictionnaire de mathématiques récréatives Spirale

Spirale

Figure formée en écrivant la suite des entiers consécutifs selon les règles suivantes. On écrit d’abord 1 au centre. On écrit 2 à sa droite et les entiers suivants dans le sens des aiguilles d’une montre. Lorsqu’un entier complète le cercle, on place toujours le suivant à la droite de celui-ci. Voici le tableau :

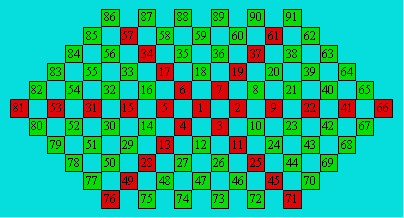
Cette spirale contient six suites arithmétiques de degré 2 dont le premier terme est 1. Les voici :

Rang n	1	2	3	4	5	6	7	8	9	10
1^e	1	2	9	22	41	66	97	134	177	226	3n² - 8n + 6
2^e	1	3	11	25	45	71	103	141	185	235	3n² - 7n + 5
3^e	1	4	13	28	49	76	109	148	193	244	3n² - 6n + 4
4^e	1	5	15	31	53	81	115	155	201	253	3n² - 5n + 3
5^e	1	6	17	34	57	86	121	162	209	262	3n² - 4n + 2
6^e	1	7	19	37	61	91	127	169	217	271	3n² - 3n + 1
Raison	0	1	2	3	4	5	6	7	8	9	n - 1

Les nombres de la sixième suite du tableau sont des centrés D2 hexagonaux.

Index : S