Solution 1. On procède à rebours. Quand on prend le tiers, on inverse 2/3, ce qui donne 3/2. Quand on prend le quart, on inverse 3/4, ce qui donne 4/3. On fait : 100 – 2 = 98, 98 × 3/2 = 147, 147 – 3 = 144 et 144 × 4/3 = 192. Pascale a acheté 192 roses.

Solution 2. Soit x le nombre de joueurs de 12 ans, y le nombre de joueurs de 11 ans et z le nombre de joueurs de 10 ans. On peut écrire : 4x + 3y + 2z = 100 et x + y + z = 36. En multipliant par 2 la deuxième équation et en soustrayant de la première, on obtient : 2x + y = 28. La plus grande valeur possible de x est 13. Alors, y = 2 et z = 21. La somme est 36. Les récipiendaires sont 13 joueurs de 12 ans, 2 joueurs de 11 ans et 21 joueurs de 10 ans.

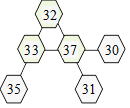
Solution 3. Il y a en tout 198 noisettes. Soit A le total des noisettes des cellules rouges et B, le total des trois autres cellules. Comme les trois nombres de A appartiennent chacun à deux rangées et qu’il y a 3 rangées, on peut écrire : 2A + B = 300. Par ailleurs, A + B = 198. D’où, A = 102. La somme des nombres des trois cellules rouges est 102. On doit trouver 102 noisettes dans les cellules rouges. On peut placer les noisettes ainsi :

Solution 4. S’il y avait là 4 jeunes, il y aurait 4 × 3 = 12 cartes. S’il y avait 5 jeunes, il y aurait 5 × 4 = 20 cartes. On doit multiplier deux nombres consécutifs. On fait : 11 × 10 = 110. Il y a 11 jeunes présents. On ajoute les 3 absents. Tante Lorraine a 14 neveux et nièces.

Solution 5. Soit x le nombre de femmes adultes, y le nombre de jeunes femmes et z le nombre d’adolescentes. On peut écrire : 2x + y/2 + z/4 = 100 ou 8x + 2y + z = 400 et x + y + z = 100. On multiplie la deuxième équation par 2 et on soustrait de la première. On obtient : 6x – z = 200. Si z = 40, alors x = 40. À rejeter, car il doit y avoir plus d’adolescentes que de toutes autres. Si z = 46, alors x = 41. Dans ce cas, y = 13. À rejeter pour la même raison. Si z = 52, alors x = 42, puis y = 6. Il y a 42 femmes adultes, 6 jeunes femmes et 52 adolescentes.

Solution 6. On divise successivement 99 par un entier qui correspond au nombre de petits lutins. Il faut que le quotient soit un entier ou un entier et demi. Si le résultat est un entier, il est le terme du milieu de la suite. Si le résultat est un entier et demi, il est la somme des deux termes du milieu.

• On divise 99 par 2. Le quotient est 49,5. La suite est 48, 51. À rejeter, car le premier doit recevoir moins de 25 papillotes.

• On divise 99 par 3. Le quotient est 33. La suite est 30, 33, 36. À rejeter pour la même raison.

• On divise 99 par 6. Le quotient est 16,5. La suite est 9, 12, 15, 18, 21, 24.

• On divise 99 par 9. Le quotient est 11. La suite est -1, 2, 5, 8, 11, 14, 17, 20, 23. À rejeter, car le premier ne peut pas recevoir un nombre négatif de papillotes.

Il y avait 6 petits lutins qui recevront 9, 12, 15, 18, 21, 24 papillotes.

Solution 7. On place respectivement 1, 2, 3 et 4 dans les cases des extrémités de la croix pour que la somme soit 5 dans chaque rangée. On place respectivement 5, 6, 7 et 8 autour du centre pour que la somme soit 13 dans chaque rangée. On fait : 100 – 5 – 13 = 82. Le plus grand nombre qui peut être placé au centre est 82.

Solution 8. Puisque la somme des nombres des quatre coins est 100, on fait 100 ÷ 4 = 25 : c’est le nombre du milieu du carré. La somme de chaque rangée est 25 × 3 = 75. De plus, 25 est le nombre du milieu de la suite des neuf nombres consécutifs. Il doit y avoir quatre nombres avant 25 et quatre nombres après. La suite est 21, 22, 23, 24, 25, 26, 27, 28, 29. On complète le carré avec ces données.

Solution 9. Dans la première distribution, chacun reçoit 10 cerises. Dans la deuxième distribution, le premier enfant a reçu x cerises, le deuxième (x + 1) cerises, jusqu’au dernier qui a reçu (x + 9). La somme est (10x + 45). En ajoutant les 100 cerises lors de la première distribution, on obtient (10x + 145). D’après la dernière condition, on écrit : (10x + 145) – (10 + x + 9) = 171. D’où, x = 5. On remplace x par 5 dans (10x + 145). Sophie avait 195 cerises.

Solution 10. On procède à rebours. Avant le quatrième kiosque, Ophélie avait 94 médaillons, soit 100 – 6. Avant le troisième, elle en avait 188, soit 94 × 2. Avant le deuxième, elle en avait 196, soit 188 + 8. On fait : 196 ÷ 2. Au début, Sophie avait 98 médaillons.  

Solution 11. On fait : 100(1/2 + 1/3 + 1/4). Lucie a parcouru 108 1/3 mètres. Elle a dépassé de 8 1/3 mètres son point de départ. On fait : 100(1/2 + 1/4 + 1/6). Martin a parcouru 91 2/3 mètres. Il lui manque 8 1/3 mètres pour atteindre son point de départ. À la fin du parcours, les deux amis sont à la même distance de leur point de départ.

Solution 12. Pour trouver le diviseur commun entre 533 et 598, on fait : 598 – 533 = 65. Les facteurs de 65 sont 5 et 13. Or, 5 n’est pas un diviseur de 533 et de 598. D’où, 13 est le diviseur commun de ces deux nombres. On fait : 533 ÷ 13 = 41 et 598 ÷ 13 = 46. Adam a 41 éléphants, Carl 13 et Benoît 46.

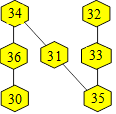
Solution 13. La somme des 7 nombres est 231. Soit Z la somme des nombres autres que A et B. Comme A et B apparaissent sur deux rangées, on peut écrire : 2(A + B) + Z = 300. Par ailleurs, A + B + Z = 231. On soustrait les deux équations. On obtient : A + B = 69. La somme des nombres des cellules marquées A et B sera 69. On peut distribuer les nombres ainsi :

Solution 14. Comme la somme de chaque rangée est 100, le nombre du milieu est 33 1/3. On complète par calculs. Le carré magique est :

Solution 15. Soit x le nombre de médailles en chocolat et y le nombre de médailles en caramel. On fait : 10x + 8y = 100. En simplifiant, on obtient : 5x + 4y = 50. On donne successivement à x les valeurs 1, 2, 3, 4, … On trouve : x = 6 et y = 5. L’école a remporté 6 médailles en chocolat et 5 en caramel.

Solution 16. On procède à rebours. On fait : 100 + 12 = 112. Avant la quatrième partie, Marcelle avait 112 pommes. On fait : 112 ÷ 2 = 56. Après la troisième, elle en avait 56. On fait : 56 + 12 = 68. Avant la troisième, elle en avait 68. On fait : 68 ÷ 2 = 34. Après la deuxième, elle en avait 34. On fait : 34 + 12 = 46. Avant la deuxième, elle en avait 46. On fait : 46 ÷ 2 = 23. Après la première, elle en avait 23. On fait : 23 + 12 = 35. Au début, Marcelle avait 35 pommes.

Solution 17. À titre d’approximation, on extrait la racine carrée de 100. Cela donne 10. On fait : 10 × 13 = 130. À rejeter. On fait : 9 × 12 = 108. La carte contient 12 lignes parallèles.

Solution 18. Le premier château de chaque rangée horizontale est successivement de rangs 1, 3, 6, 10. Le terme général de cette suite est n(n + 1)/2 où n est le rang. On fait : (n² + n)/2 = 100, soit n² + n – 200 = 0. En résolvant l’équation, la racine positive est 13,65. Le rang de la rangée horizontale est la partie entière. Le premier nombre de cette rangée est 91. On fait : 100 – 91 + 1 = 10. Bref, le 100^e château est le 10^e de la 13^e rangée horizontale.

Solution 19. Soit a, b, c et d le nombre de livres par tablette de haut en bas. On suppose qu’il y a 1 livre sur la tablette du haut. Alors, a = 1, b = 46, c = 2 et d = 5. Il y aurait en tout 54 livres. Si le nombre de livres de a augmente de 1, celui de b diminue de 1, celui de c augmente de 1, celui de d augmente de 1. Il y a alors augmentation de 2 au total. On fait : (100 – 54)/2 = 23. Par rapport à la première hypothèse, pour a, on augmente de 23. Pour b, on diminue de 23. Pour c, on augmente de 23. Pour d, on augmente de 23. Du haut en bas, il y a 24, 23, 25, 28 livres.

Solution 20. On construit un tableau dans lequel on suppose 1, 2 et 3 lancers à l’extérieur de la cible, H étant une hypothèse.

Le nombre total de points diminue de 6 d’une hypothèse à l’autre. On fait : (136 – 100)/6 + 1 = 7. Le total, soit 100, serait à la septième hypothèse. Jade a atteint le centre de la cible 8 fois.

Solution 21. On procède à rebours. Quand on parcourt un tiers d’un trajet, il en reste 2/3. La fraction inverse est 3/2. On fait : (100 + 4) × 3/2 = 156, (156 + 6) × 3/2 = 243, (243 + 5) × 3/2 = 372. La randonnée est de 372 kilomètres.

Solution 22. Dans la première rangée, le nombre augmente successivement de 2, 3, 4, 5. Le 50^e terme provient d’une augmentation de 50. On a une suite de 49 termes. La somme des termes est : 49(2 + 50)/2 = 1274. On additionne le premier terme 3. Le 50^e terme de la première rangée est 1277. Dans la seconde rangée, chaque nombre de même rang provient du nombre de la première rangée, multiplié par 3 et augmenté de 1. On fait : 1277 × 3 + 1 = 3832. C’est le 50^e nombre de la deuxième rangée. On fait : 3832 – 1277 = 2555. La différence entre les deux derniers numéros est 2555.

Solution 23. Soit x le montant reçu par Liane. Clara a reçu (100 + x/2). Mathieu a reçu (100 + x/3). Isaac a reçu (100 + x/6). En tout, les quatre ont reçu (300 + 2x). Soit y l’avoir d’Eusèbe. Liane a reçu 100 + (y – 100)/4, soit x = (y + 300)/4. On remplace x par cette valeur dans (300 + 2x). On obtient (900 + y)/2. On fait : (900 + y)/2 = y. D’où, y = 900. Eusèbe avait 900 florins.

Solution 24. On fait : 3A – 18 + 3B – 1 = 2A + 5 + 3B – 3. On tire : A = 21. On fait : 3B – 1 + C + 9 = 2C – 1 + 3B – 3. On tire : C = 12. On obtient la valeur de B qui est 15 en remplaçant A et C par leur valeur dans n’importe laquelle rangée. La grille remplie est :

Solution 25. La somme des unités des nombres manquants est 14. Une seule combinaison est possible : (3, 5, 6). Les dizaines sont (1, 2, 4). On peut écrire : 16 + 13 + 25 + 46 = 100. Il y a une seule possibilité.

Solution 26. Sur la première ligne, on peut lire 5, 13, 21 aux colonnes 1, 3, 5. La différence est 8 entre chaque terme de la suite. Le terme général est (8n – 3). On fait : 8n – 3 = 100. D’où, n = 12,875. Lorsque n = 13, le terme est 101. Pour connaître le rang de la colonne, on multiplie par 2 et on soustrait 1. On fait : 13 × 2 – 1 = 25. Le nombre 101 apparaît sur la première ligne de la 25^e colonne. Le nombre 100 apparaît sur la deuxième ligne de la 25^e colonne.

Solution 27. On procède à rebours. On fait successivement : 100 + 8 = 108, 108 × 2 = 216, 216 + 6 = 222, 222 × 4/3 = 296, 296 + 5 = 301 et 301 × 8/7 = 344. On fait : 344 – 100 = 244. La distance parcourue pendant les trois premières heures est de 244 mètres.

Solution 28. En 6 jours, Laurie mange 18 noisettes, Mathis 21 et Florence 20 : ce qui donne 59 noisettes. En 12 jours, Laurie mange 36 noisettes, Mathis 42 et Florence 40 : ce qui donne 118 noisettes. Le 12^e jour, ensemble les trois ont mangé 20 noisettes, ce qui fait un total de 98 pour le 11^e jour. Ils ont donc atteint le total de 100 noisettes le 12^e jour. Les trois personnes auront mangé au moins 100 noisettes le 23 octobre.

Solution 29. La figure qui a 100 cercles à la base est la 101^e. Le nombre de cœurs est successivement 6, 9, 12, 15, etc. Soit n le rang des figures, le terme général est (3n + 3). On remplace n par 101. On obtient 306. La dernière figure contient 306 cœurs.

Solution 30. On fait : 100 ÷ 9 = 11 reste 1. Le dernier chiffre de la première ligne est 1. Le dernier chiffre de la deuxième ligne est 2. Le dernier chiffre de la neuvième ligne est 9. Le dernier chiffre de la 99^e ligne est 9. Le dernier chiffre de la 100^e ligne serait 1.

Solution 31. La suite du premier terme de chaque ligne est 3, 5, 8, 12, ... Le terme général de la suite est (n² + n + 4)/2. Si n = 13, le premier terme est 93. Si n = 14, le premier terme est 107. Le dernier terme de la 13^e ligne est 106. Connaissant le premier et le dernier terme de cette suite, on fait : (93 + 106)/2 = 99,5. La moyenne des nombres de la ligne où se trouve 100 est 99,5.

Solution 32. On compte quatre rangées où la somme est 100. Le total est 400. La somme des trois nombres donnés est 94. Comme les nombres sont à l’intersection de deux rangées, on multiplie par 2. Le résultat est 188. On fait : 400 – 188 – 154 = 58 et 58 ÷ 2 = 29. Le nombre 29 devra apparaître dans la cellule Z.

Solution 33. Si A + A + E = 10, alors B + N + N = 9. Le seul triplet possible pour 9 est (5, 2, 2). On peut avoir : 53 + 23 + 24 = 100. D’où N peut être égal à 2. Si A + A + E = 20, alors B + N + N = 8. Les triplets possibles pour 8 sont (2, 3, 3) et (4, 2, 2). On peut avoir notamment : 28 + 38 + 34 = 100 et 46 + 26 + 28 = 100. Les valeurs possibles de N sont 2 et 3.

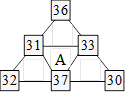
Solution 34. La somme totale des nombres des trois petits triangles marqués S est 300. On fait : 300 – 98 = 202. Comme chacun des sommets de A est l’intersection de ces trois triangles, on divise 202 par 2. Le résultat est 101. La somme des sommets du petit triangle marqué A est 101. On peut avoir la configuration suivante :

Solution 35. Le premier nombre qui est multiple de 3 varie de 3 à 48. Cela fait 16 sommes. Le deuxième nombre qui est multiple de 3 varie de 99 à 51. Cela fait 17 sommes. On peut décomposer 100 en 33 couples.

Solution 36. Hélice est en congé pendant neuf jours. Elle mange 45 avelines. Sauf les dimanches, elle travaille pendant 17 jours. Elle reçoit 51 avelines. Elle travaille quatre dimanches. Elle mange 8 avelines. On fait 100 – 45 + 51 – 8 = 98. Hélice aura 98 avelines le 1^er mars au soir.

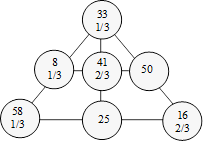
Solution 37. Le total des nombres des deux rangées horizontales est 200. On fait : 200 ÷ 3 = 66 2/3. Si on exclut le cercle supérieur, c’est la somme des deux autres nombres pour chaque rangée diagonale et verticale. On fait : 100 – 66 2/3 = 33 1/3. Le nombre qui doit être placé dans le cercle supérieur est 33 1/3. Voici un exemple de configuration :

Solution 38. Soit a le nombre de pamplemousses de la première boîte, b le nombre de la deuxième boîte et c le nombre de la troisième boîte. Alors, a² + b² = 2669 et b² + c² = 1954. En soustrayant les deux égalités, on a : a² – c² = (a + c)(a – c) = 715. Les facteurs de 715 sont (1, 715), (5, 143), (11, 65) et (13, 55). On additionne les nombres de chaque facteur et on divise par 2 : c’est la valeur de a. De a, on soustrait le plus petit nombre pour obtenir c. Seul, (11, 65) est possible. On fait : a = (11 + 65)/2 = 38 et c = 38 – 11 = 27. Comme il y a 100 pamplemousses en tout, b = 35. La première boîte contient 38 pamplemousses, la deuxième 35 et la troisième 27.

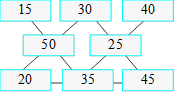
Solution 39. Glen a dépensé 35 roubles, car Claude et Émilie ont dépensé 65 roubles. Chaque groupe suivant a dépensé 65 roubles : Abel et Denys, Claude et Émilie, Flavia et Hélène. On fait : 35 + 3 × 65 = 230. En tout, les 8 amis ont dépensé 260 roubles. On fait : 260 – 230 = 30. Barbara a dépensé 30 roubles. Voici une configuration possible :

Solution 40. On procède à rebours. On fait 100 × 6 = 600, 600 + 6 = 606, 606 ÷ 6 = 101 et 101 – 6 = 95. Gervaise a vendu 95 melons depuis le matin.

Solution 41. Soit M le terme du milieu. On fait : 100 + M = 104 + 103. D’où, M = 107. On fait : 107 × 3 = 321. La somme dans chaque rangée est 321. On complète par calculs. Le carré est :

Solution 42. On continue la suite jusqu’à ce qu’on ait un nombre de trois chiffres. On peut écrire : 75, 86, 98, 111. Il y a 12 nombres de deux chiffres. Parvenu à 98, on aura donc écrit 24 chiffres. Il reste 76 chiffres à écrire. On fait : 76 ÷ 3 = 25 reste 1. Le 100^e chiffre sera le premier chiffre du 26^e nombre de trois chiffres ou du 38^e nombre de la suite. Le terme général de la suite est (n² + n + 40)/2. Si n = 38, le nombre est 761. Le 100^e chiffre est 7.

Solution 43. À partir de la première opération, la suite du nombre de pruneaux dans le sac est 7, 5, 10, 8, 13, 11, 16, 14, … On retient la suite 7, 10, 13, 16 … Soit n le rang, le terme général est (3n + 4). On fait : 3n + 4 = 100. D’où, n = 32. Il y a 32 opérations d’ajout et 31 opérations d’extraction. Roméo effectuera 63 opérations.

Solution 44. Dans une grille 3 × 3, on a 3 bâtonnets bleus horizontaux sur 2 lignes et 3 bâtonnets bleus verticaux sur 2 colonnes : ce qui fait 12 bâtonnets bleus. Dans une grille 10 × 10, on aura 10 bâtonnets bleus horizontaux sur 9 lignes et 10 bâtonnets bleus verticaux sur 9 colonnes : ce qui fait 180 bâtonnets bleus. Zoé aura besoin de 180 bâtonnets bleus.

Solution 45. Quand le nombre de sacs de trois ananas augmente de 4, le nombre de sacs de quatre ananas diminue de 4. On a : (4, 22), (8, 19), (12, 16), (16, 13), (20, 10), (24, 7), (28, 4), (32, 1) où la première coordonnée désigne des sacs de 3 ananas et l’autre des sacs de 4 ananas. Le couple (16, 13) répond à la deuxième condition. Nathaniel recevra 16 sacs de trois ananas et 13 sacs de quatre ananas.

Solution 46. Comme il resterait 2 tartes, on fait : 100 – 2 = 98. Selon les conditions, il y aurait au moins 14 clients. On fait : 98 ÷ 14 = 7. Chaque client recevrait 7 tartes. On fait : 6 × 7 + 1 = 43 et 8 × 7 + 1 = 57. Il y a 43 tartes aux raisins et 57 tartes aux bleuets.

Solution 47. Pour tout âge jusqu’à 11 ans, le résultat de la multiplication (première condition) est inférieur à 100. La différence (troisième condition) ne pourrait pas être 100. On suppose que la fille a 12 ans. On peut écrire : (12 – 5)(12 + 5) – (12 – 5 + 12). Le résultat est 100. La fille a 12 ans.

Solution 48. On trouve six inscriptions consécutives ayant la même lettre. On fait : 100 ÷ 6 = 16 2/3. On trouve 16 groupes complets de six cases. La dernière lettre sera la 17^e, soit Q. Le premier nombre pour chaque lettre est 2, 4, 6, 8, 10, ... Le premier nombre du 17^e groupe sera 34. Q34 est au 97^e rang. Suivent Q37, Q40, Q43. La 100^e case devra recevoir Q43.

Solution 49. Comme Paul retire 22 litres du premier tonneau à la fin, il reste 78 litres dans les deux tonneaux. Puisque les deux tonneaux ont la même quantité, chaque tonneau a 39 litres. Le premier en avait 61 avant le retrait du 22 litres. On procède à rebours. On fait : 39 × 4/3 = 52. Il y a eu un transfert de 13 litres si bien que le premier tonneau en avait 48. On fait : 48 × 4/3 = 64. Le premier tonneau contenait 64 litres et le deuxième 36 litres.

Solution 50. La somme totale des nombres est 108. On fait 108 ÷ 9 = 12 : c’est l’élément central. On fait 108 ÷ 3 = 36 : c’est la somme de chaque ligne, colonne et diagonale. Le nombre au centre de la troisième ligne est 16 : c’est le plus grand. Entre 8 et 16, il y a sept nombres consécutifs : 9, 10, 11, 12, 13, 14 et 15. On distribue ces nombres à part le 12 qui est déjà au centre. On obtient le carré magique suivant dans lequel on peut intervertir les nombres de la première et de la troisième colonne :

Solution 51. Avant d’arriver chez son voisin, Lucas doit avoir 120 pommes. On fait : 120 × 4/3 = 160, 160 × 5/4 = 200 et 200 × 6/5 = 240. Lucas devra acheter 240 pommes.

Solution 52. Le premier stylo d’encre noire par groupe est de rang 1, 3, 6, 10, 15, … On a la suite des nombres triangulaires. Or, autour de 100, les deux nombres triangulaires sont 91 et 105. Les stylos de rangs 90 et 104 sont rouges. La couleur de l’encre du 100^e stylo sera noire.

Solution 53. Chaque ensemble exige 6 cases. On fait : 100 × 6 = 600. On extrait la racine carrée de 600. Cela donne 24,49. Comme on place un cœur dans les cases 1, 7, 13, 19, …, le terme général est 6n – 5. On fait : 6n – 5 = 24². D’où, n = 96,8. Dans une grille 24 × 24, on pourra disposer 96 cœurs et 96 trèfles. On fait : 6n – 5 = 25². D’où, n = 105. Dans une grille 25 × 25, on pourra disposer 105 cœurs et 104 trèfles. La plus petite grille carrée est de 25 × 25.

Solution 54. Chaque rangée horizontale contient 100 allumettes. Il y a 101 rangées horizontales. Cela donne 10 100 allumettes. Chaque rangée verticale contient 100 allumettes. Il y a 101 rangées verticales. Cela donne 10 100 allumettes. On fait : 20 200 ÷ 100 = 202. En tout, Nathaniel aurait besoin de 202 boîtes d’allumettes.

Solution 55. Sans compter les deux colonnes des extrémités, on aura un rectangle 104 × 3. Sur les deux premières lignes, on compte 103 carrés 2 × 2. Il en est de même sur les deux dernières lignes. Cela fait 206 carrés. En tenant compte des extrémités, on compte un carré 2 × 2 à gauche et un autre à droite. On pourra compter 208 carrés 2 × 2 dans la figure prolongée.

Solution 56. On trouve l’inverse de chaque donnée numérique et on additionne. On a : 2 + 1 + 2/3 + 1/2 = 12/6 + 6/6 + 4/6 + 3/6 = 25/6. Comme le numérateur de la somme est 25, on multiplie par 4, le numérateur de la fraction correspondant à chacun des élèves. On fait : 12 × 4 = 48, 6 × 4 = 24, 4 × 4 = 16 et 3 × 4 = 12. Anne recevra 48 points, Jacob 24 points, Karl 16 points et Mélodie 12 points.

Solution 57. La première ligne des sommes comporte les nombres de 2 à 101. La somme de ces nombres est (2 + 101)100/2 = 5150. Il y a une différence de 100 entre les sommes de chaque ligne inférieure. La dernière ligne des sommes comporte les nombres de 101 à 200. La somme est (101 + 200)100/2 = 15 050. Les sommes forment une suite de 100 termes dont le premier terme est 5150 et le dernier 15 050. On fait : (5150 + 15 050)100/2 = 1 010 000. La somme des nombres de la table est 1 010 000.

Solution 58. La somme de chaque rangée étant 291, le nombre du milieu de la grille est 97. C’est aussi le nombre du milieu de la suite de nombres consécutifs. Le plus petit nombre est 93 et le plus grand est 101. On peut disposer les nombres ainsi.

Solution 59. Le total des sommes des trois côtés est 300. La somme des nombres de 5 à 45 est 225. On fait : 300 – 225 = 75, ce qui est la somme des nombres des trois cellules des coins. Sur le côté de gauche, les deux cellules des coins ont une somme de 50. On fait : 75 – 50 = 25. La cellule du coin inférieur droit aura le numéro 25.

Solution 60. La première ligne des produits comporte les nombres de 1 à 10. La somme est (1 + 10)10/2 = 55. La deuxième ligne des produits est le double de la première ligne, soit une somme de 110. La troisième ligne des produits est le triple de la première ligne, soit une somme de 165. La dernière ligne des produits est 10 fois la première ligne, soit une somme de 550. Il y a 10 sommes. On fait : (55 + 550)10/2 = 3025. La somme des produits est 3025.

Solution 61. Soit A la somme des nombres des quatre coins et B la somme des quatre autres nombres. On peut écrire : A + B = 260. Il y a quatre rangées dont la somme est 100 : cela fait 400. Comme les quatre cases du centre apparaissent dans deux rangées, on peut écrire : A + 2B = 400. D’où, A = 120 et B = 140. On fait : 120 – (25 + 35) = 60. La somme des nombres des deux autres coins opposés est 60.

Solution 62. Sur la troisième ligne, on peut placer le quadruplet (5, 20, 30, 45). La somme des nombres de chaque rangée verticale doit être : 100 × 3/4 = 75. Dans la première colonne, on peut placer le triplet (15, 20, 40). Seul 20 appartient aux deux ensembles. On place 20 dans le coin inférieur gauche. On pourrait avoir :

Solution 63. Comme la somme est 100 dans chaque rangée horizontale, la somme des nombres à placer est 300. Dans les deux rangées verticales de trois cellules, la somme des nombres est 200. On fait : 300 – 200 = 100. La somme des nombres des trois cellules des extrémités des rangées horizontales est 100. On fait : 100 – (19 + 46) = 35. Le nombre qui doit être placé au début de la deuxième rangée horizontale est 35.

Solution 64. On compte le nombre d’ampoules par branche : 100 + 99 + 99 = 298. Comme on a quatre branches, on fait : 298 × 4 = 1192. On a compté deux fois les quatre ampoules de jonction des branches. On fait : 1192 – 4 = 1188. Roxanne aura besoin de 1188 ampoules.

Solution 65. Le premier prunier de la rangée 1 est le 1^er arbre. Celui de la rangée 2 est le 3^e arbre. Celui de la rangée 3 est le 6^e arbre. Celui de la rangée 4 est le 10^e arbre. On a la suite : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105. Le premier prunier de la rangée 13 est le 91^e arbre. On fait : 100 – 91 + 1 = 10. Le 100^e prunier est le 10^e de la rangée 13.

Solution 66. Le tableau donne le résultat en fonction d’un nombre pair atteint.

Le résultat est égal à la moitié de la somme du dernier nombre et de 100. On fait : (50 + 100)/2 = 75. Lorsque Robert aura écrit 50, le résultat sera 75.

Solution 67. Le nombre de personnes est successivement 3, 7, 11, 15, 19, … Le terme général de la suite est (4n – 1). On fait : 4n – 1 = 100. D’où, n = 25,25. Si n = 25, la table qui correspond à celle du 25^e rang reçoit 99 personnes. Celle qui correspond au 26^e rang contient 103 personnes. C’est là que se trouve le 100^e invité. Il y aurait 103 personnes autour de la table où on pourrait placer le 100^e invité.

Solution 68. La somme des nombres des quatre rangées horizontales est 400. Lorsque la somme est 400, la moyenne d’une suite de 10 nombres de différence 4 est 40. Les deux termes du milieu sont 38 et 42. La suite est : 22, 26, 30, 34, 38, 42, 46, 50, 54, 58. En additionnant trois de ces nombres, on ne peut pas trouver une somme de 100. Il est donc impossible de remplir la figure.

Solution 69. La somme des huit nombres est 260. La somme des nombres des deux cellules de droite est la même que celle des cellules du haut, soit 60. On fait : 260 – (60 + 60) = 140. La somme des nombres devant être placés dans les quatre cellules rouges est 140.

Solution 70. Soit A et B les deux nombres absents de la rangée du bas. Dans la figure, A est additionné trois fois. B est additionné trois fois. On écrit : 100 = 10 + 3A + 3B + 21. D’où, A + B = 23. On fait : 10 + 23 + 21 = 54. La somme des nombres de la rangée du bas est 54.

Solution 71. On place 100, 101 et 102 dans les cellules des angles. Les sommes de ces nombres sur chaque côté sont 201, 202 et 203. La somme des six nombres de 103 à 108 est 633. On fait : 201 + 202 + 203 + 633 = 1239 et 1239 ÷ 3 = 413. La plus petite somme par rangée est 413.

Solution 72. On compte 100 carrés 1 × 1, 81 carrés 2 × 2, 64 carrés 3 × 3, 49 carrés 4 × 4, 36 carrés 5 × 5, 25 carrés 6 × 6, 16 carrés 7 × 7, 9 carrés 8 × 8, 4 carrés 9 × 9 et 1 carré 10 × 10. Au total, on compte 385 carrés de toute grandeur.

Solution 73. On compte six rangées où la somme est 100. Le total est 600. Les deux rangées verticales ont une somme de 200. Comme chaque case est l’intersection de deux rangées, cela compte pour 400. Il reste 200 pour les quatre cases qui appartiennent à une seule rangée. On fait : 33 + 58 + 49 + A = 200. D’où, A = 60. Voici un exemple de distribution :

Solution 74. Le carré magique composé de nombres pairs consécutifs à partir de 2 et dont la somme par rangée est la moindre est :

On additionne 96 à chacun des nombres. On obtient le carré magique dont la somme par rangée est la plus petite possible, soit 318.

Solution 75. La suite de Fibonacci est : 1, 1, 2, 3, 5, 8, 13, 21, 34. Toute autre suite basée sur ce modèle est définie en multipliant chacun des nombres de cette suite par le nombre de départ. On fait : 510 ÷ 102 = 5 et 5 × 3 = 15. Le nombre de départ sera 15.

Solution 76. La somme des nombres est 999. On divise par 3. On obtient 333 : c’est la somme des nombres de chaque rangée. On divise 333 par 3. Le résultat 111 est le nombre du milieu. On complète et on obtient :

Solution 77. On fait : 100 – 28 = 72 et 72 ÷ 2 = 36. Or, 100 – 36 = 64. Il y a 64 lièvres dans le carré vide. Comme chaque lièvre des quatre coins est compté deux fois et que le carré a quatre côtés, on fait : 64 + 4 = 68 et 68 ÷ 4 = 17. Il y a 17 lièvres sur chaque côté du carré vide.

Solution 78. La suite est 10, 11, 14, 19, 20, 23, 28, 29, … En excluant le sac du début, à la fin de chaque groupe de 3 sacs, le nombre de noisettes a augmenté de 9 par rapport au dernier élément du groupe précédent. On fait : (100 – 10)/9 = 10. On a 10 groupes de 3 sacs, ce qui fait 30 sacs. On ajoute le premier sac. Trente-et-un sacs sont nécessaires.

Solution 79. Le nombre de tuiles est successivement 4, 8, 12, 16, 20, etc. La figure composée de 100 tuiles est la 25^e. Chacun des côtés du carré intérieur mesure 49 centimètres. On fait : 49 × 4 = 196. Le périmètre du carré intérieur d’une figure qui comprend 100 tuiles est de 196 centimètres.

Solution 80. Soit x le montant possédé par Zénon. Il a donné x/4. Gertrude a donné aussi x/4. Il reste 3x/4 à Zénon. Il a donné : 3x/4 × 1/3 = x/4. Gertrude a donné x/4. Le garçon a : 4x/4 = 100. D’où, x = 100. Zénon avait 100 $.

Solution 81. La clé réside dans le fait que le carré est sectionné en quatre carrés 2 × 2. Comme le montre le petit carré du coin inférieur droit, dans ces petits carrés, on retrouve une colonne dont la somme est 48 et dont l’autre est 52. On commence par compléter la diagonale de gauche avec 15. On fait 52 – 15 = 37. On l’écrit sous 15. En continuant, on obtient le carré magique suivant.

Solution 82. À cause de la dernière proposition, le montant total dépensé est de 555 euros. On fait 555 – 225 = 330. Les filles dépensent ensemble 330 euros. On fait : 555 ÷ 100 = 5,55. La dépense moyenne par personne est de 5,55 euros. Les garçons ont dépensé chacun 5 euros et les filles chacune 6 euros. On fait : 225 ÷ 5 = 45. On fait : 330 ÷ 6 = 55. Il y a 45 garçons et 55 filles.

Solution 83. Le nombre d’oranges par couronne est successivement 6, 12, 24, 48, soit un total de 90. En ajoutant l’orange de départ, on en a 91. Il reste 9 oranges pour la dernière couronne. La 100^e orange serait bleue.

Solution 84. On illustre les quatre premières étapes par un tableau.

Soit n le rang des arbres, la distance parcourue est 2(n + 2). Si n = 100, alors 2(100 + 2) = 204. On a une suite de 50 termes dont le premier est 8 et le dernier, 204. On fait : (8 + 204)50/2 = 5300. Le fils doit parcourir 5300 mètres.

Solution 85. Dans chaque rangée horizontale et verticale, on peut tracer 8 droites. Comme il y a 20 rangées, on fait : 20 × 8 = 160. Obliquement, de gauche à droite, on peut tracer 1, 2, 3, 4, 5, 6, 7, 8, 7, 6, 5, 4, 3, 2, 1 droites, soit un total de 64 droites. Obliquement, de droite à gauche, on peut aussi tracer 64 droites. On fait : 160 + 64 + 64 = 288 droites. Sara pourra tracer 288 droites.

Solution 86. Voici le nombre de traits nouveaux et cumulatifs en regard du rang de chaque losange :

Le nombre de traits du losange de rang pair est successivement : 7, 12, 17, 22, 27, … Le terme général de rang n est 5n + 2. On fait : 5 × 50 + 2 = 252. Le 50^e terme de cette suite est 252. On aurait besoin de 252 traits droits pour tracer cette figure.

Solution 87. On fait : 100 × 100 ÷ 6 = 1666 2/3. Théoriquement, on pourra répartir au plus 1666 pièces. Il resterait 4 cases libres dans la grille. Pour vérifier ce résultat, on compose un rectangle 5 × 6, comme il est montré dans la partie supérieure de la grille ci-dessous. On applique ce rectangle vers la droite et vers le bas. On couvre une grille 100 × 96, ce qui donne 1600 pièces. Il reste une lisière de 100 × 4. On dispose les pièces comme il est montré dans la partie inférieure. On peut y placer 66 pièces. En tout, on peut disposer 1666 pièces et il reste quatre cases libres comme il est montré en bas à droite.

Solution 88. Pour l’hexagone du sommet, on a besoin de 6 cure-dents. Pour la deuxième rangée, on a besoin de 9 autres cure-dents. Pour la troisième rangée, on a besoin de 12 autres cure-dents. Pour la quatrième rangée, on a besoin de 15 autres cure-dents. Le terme général de la suite est (3n + 3). Pour la 100^e rangée, on aura besoin de 303 cure-dents. On fait : (6 + 303)100/2 = 15 450. On aurait besoin de 15 450 cure-dents.

Solution 89. La première couronne exige un carré 4 × 4. La deuxième couronne exige un carré 6 × 6. La troisième couronne exige un carré 8 × 8. Le terme général de la suite 4, 6, 8, 10, … est (2n + 2). Si n = 100, la 100^e couronne exigera un carré 202 × 202. On fait : 202 × 4 = 808. On soustrait 4, ce qui correspond aux oranges des coins. Laurie aurait besoin de 804 oranges pour composer la 100^e couronne.

Solution 90. Le cavalier se déplace alternativement de (1, 2) et de (2, 1) comme dans l’exemple. Au deuxième saut, il atteint la case (4, 4). Au quatrième saut, il atteint la case (7, 7). Au sixième saut, il atteint la case (10, 10). Au huitième saut, il atteint la case (13, 13) et ainsi de suite. Le nombre 100 appartient à la suite : 4, 7, 10, 13, 16, etc. Il est le 33^e terme. Le cavalier fait 2 sauts par séquence. On multiplie 33 par 2. Le cavalier fait 66 sauts pour atteindre la case du coin inférieur gauche.

Solution 91. On suppose que la grille n’est pas rognée. Dans chaque groupe de trois lignes, on compte 98 carrés 3 × 3. On a 98 groupes de trois lignes. On fait : 98 × 98 = 9604. Dans chaque coin, on perd 4 carrés 3 × 3 : ce qui donne 16 carrés perdus. On fait : 9604 – 16 = 9588. On peut compter 9588 carrés 3 × 3 dans la croix d’une grille 100 × 100.

Solution 92. Au premier mouvement, le fou atteint la case (4, 4). Au troisième mouvement, il atteint la case (6, 8). Au cinquième mouvement, il atteint la case (8, 12). Au septième mouvement, il atteint la case (10, 16). La première coordonnée, celle qui marque l’horizontal, augmente de 2, tandis que la deuxième, celle qui marque le vertical, augmente de 4. Le nombre 100 appartient à la suite : 4, 8, 12, 16, 20, etc. Il est le 25^e terme. Les coordonnées horizontales sont 4, 6, 8, 10, 12, etc. Le 25^e terme est 52. Le fou terminera sa course sur la case (52, 100), soit sur la 52^e case de la 100^e rangée horizontale.

Solution 93. La première couronne exige 8 pièces, la seconde 14 pièces, la troisième 20 pièces. D’une couronne à l’autre, le nombre de pièces augmente de 6. En multipliant le rang de la couronne par 6 et en additionnant 2, on obtient le nombre de pièces par couronne. On fait : 100 × 6 + 2 = 602. La 100^e couronne contiendrait 602 pièces.

Solution 94. Le tableau suivant indique le nombre de groupes nouveaux et cumulatifs par rapport aux rangs des perpendiculaires sans retourner à gauche :

La suite 5, 10, 15, 20, … correspond aux perpendiculaires de rangs pairs. Soit n le rang des perpendiculaires, le terme général est 5n. En remplaçant n par 50, on obtient 250. On soustrait 2, car il n’y pas de groupes nouveaux pour la dernière perpendiculaire. On peut compter 248 groupes de deux cercles voisins reliés par une droite.

Solution 95. Soit A le premier nombre de la rangée du bas. Les autres sont successivement (A + 1), (A + 2) et (A + 3). La somme est (4A + 6). Le nombre du haut est (8A + 12), soit le double de celle du bas. La somme du bas est 100/2 = 50. Les quatre nombres consécutifs dont la somme est 50 sont 11, 12, 13, 14. La rangée du bas contient 11, 12, 13 et 14 dans cet ordre.

Solution 96. Dans les quatre figures, il y a successivement 1, 5, 11, 19 boules. L’augmentation est de 4, 6, 8 boules. Les nombres suivants sont : 29, 41, 55, 71, etc. On fait : 1 + 5 + 11 + 19 + 29 + 41 = 106. La 100^e boule est placée dans la 6^e figure. Cette figure contient 41 boules. La 100^e boule occupe le 35^e rang de la figure, soit le dernier rang de la cinquième ligne.

Solution 97. La somme des nombres de 20 à 29 est 245. Il devrait y avoir cinq rangées de somme 100, ce qui ferait 500. Comme chaque jeton appartient à deux rangées, on fait : 500 ÷ 2 = 250. Il y a un excès de 5. Voilà pourquoi, Johanne n’a pas réussi. L’ami a donc raison.

Solution 98. On suit le chemin parcouru par les nombres de 8 à 18. Les nombres progressent en diagonale de bas en haut vers la droite. Si le lieu approprié est en dehors du carré, tout élément supérieur à la première ligne est placé sur la cinquième ligne dans la même colonne et tout élément à droite de la cinquième colonne est placé dans la première colonne sur la même ligne. Lorsque le lieu est occupé, on place l'élément sous le dernier nombre inscrit. Voici la grille remplie :

Solution 99. De 1999 à 2099, il y a 25 années bissextiles. On fait : 365 × 100 = 36 500, 36 500 + 25 = 36 525 et 36 525 ÷ 7 = 5217 reste 6. Le dimanche 18 avril 2099, René aura vécu 5217 semaines et 6 jours. Le sixième jour après le dimanche est samedi. René fêtera ses 100 ans un samedi.

Solution 100. La somme des nombres par colonne est successivement 3, 8, 14, 21, 29, 38. Les nombres augmentent de 5, 6, 7, 8, 9. Entre le premier nombre et le 100^e, il y a 99 différences, soit les nombres de 5 à 103. La somme de ces nombres est 5346. On additionne le premier nombre de la suite, soit 3. On obtient 5349. La somme des nombres de la 100^e colonne est 5349.

FIN