Solutions 1 à 20

1. Petit sudoku

Sara a écrit cinq lettres dans la grille ci-dessous.

Complétez la grille avec des lettres A, B, C et D pour qu’il y ait des lettres différentes dans chaque ligne, dans chaque colonne et dans chacun des carrés 2 × 2.

2. Cavalier d’Aurélie

Aurélie prend un cavalier et trace une grille carrée 5 ´ 5. Elle déplace le cavalier en L, comme aux échecs. Les six premiers mouvements sont donnés.

Continuez à déplacer le cavalier pour qu’il visite toutes les cases, sauf la noire, une et une seule fois.

3. Carreaux de Livia

Livia dispose 12 carreaux de laine en un rectangle 3 × 4. Elle doit placer deux carreaux rouges (R), deux verts (V), quatre jaunes (J) et quatre bleus (B). Trois carreaux sont déjà posés.

Disposez les autres carreaux pour que deux carreaux voisins horizontalement, verticalement et obliquement n'aient pas la même couleur.

4. On joue au bingo

Hélène pige neuf boules de bingo dans le matériel de l’école.

Combien y a-t-il de façons d’agencer trois boules de façon que la somme des numéros soit 18 ?

5. Cellules de Viateur

Viateur a dessiné la grille ci-après formée de huit cases pâles. Il veut disposer chacun des nombres de 3 à 8 dans ces cases. La somme doit être 14 dans chaque rangée diagonale de trois cases.

Trouvez une façon de disposer les nombres de 3 à 8.

6. Triples de Cassandra

Cassandra a écrit quatre chiffres dans cette grille. Elle veut y placer trois 1, trois 2, trois 3 et trois 4. Les quatre chiffres différents doivent apparaître dans chaque rangée horizontale, verticale et diagonale.

Complétez la grille.

7. Grille de Catherine

Catherine dispose 10 et 11 dans la grille ci-après. Elle veut y écrire chacun des nombres de 3 à 9. La somme des nombres de chaque rangée horizontale, verticale et diagonale doit être 21.

Complétez la grille.

8. Cavalier de Lucie

Lucie a déplacé un cavalier de la case marquée 1 à la case 10 dans la grille ci-après. Comme on peut le constater, le cavalier forme un L quand il passe d’une case à une autre.

Continuez à déplacer le cavalier de façon à atteindre toutes les cases une et une seule fois.

9. Grille de Victor

Dans la grille ci-après, Victor a écrit des nombres de 1 à 5. Un nombre doit apparaître une seule fois dans chaque rangée horizontale et dans chaque rangée verticale.

Complétez la grille avec des nombres de 1 à 5.

10. Cartes d’Étienne

Étienne prend neuf cartes : 2, 3, 4 de carreau, 4, 5, 6 de pique, 6, 7, 8 de cœur. Il place le 6 de pique et le 8 de cœur dans la grille comme ci-après.

Disposez les sept autres cartes pour que la somme soit 15 dans chaque rangée horizontale, verticale et diagonale. De plus, on doit trouver un cœur, un carreau et un pique dans chaque rangée horizontale et verticale.

11. Coccinelles de Flora

Flora prend six coccinelles et les numérote de 2 à 7. Elle dessine la figure ci-après. Elle veut disposer les coccinelles pour que la somme soit 12 dans chaque rangée de deux ou de trois cellules reliées par une droite.

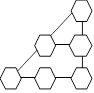
Disposez les six coccinelles.

12. Erreurs d’Alexia

Dans la grille, Alexia a écrit les chiffres 2, 3, 5, 8. Elle visait à ce que les quatre chiffres apparaissent dans chaque ligne, dans chaque colonne et dans chacune des deux diagonales. En vérifiant la grille remplie, elle remarque que chaque diagonale a deux 5.

Intervertissez deux paires de chiffres pour corriger les erreurs d’Alexia.

13. Noisettes de Nathalie

Nathalie prépare sept petits sacs de noisettes. Elle dessine la grille ci-après qui est formée de sept cases blanches. Elle place un sac de neuf noisettes dans une case. Dans les autres cases, elle désire y disposer des sacs de 3 à 8 noisettes. Il doit y avoir 17 noisettes dans chaque rangée verticale et diagonale.

Distribuez les six sacs de noisettes.

14. Petits déjeuners

Roxanne prend quatre abricots (A), quatre citrons (C), quatre mangues (M), quatre pamplemousses (P). Elle veut les placer dans une grille carrée comme ci-après. Les quatre fruits doivent apparaître sur chaque ligne et dans chaque colonne. De plus, trois pamplemousses doivent être immédiatement à droite d’un citron, et deux mangues doivent être immédiatement sous un citron. Quatre fruits sont placés.

Disposez les 16 fruits.

15. Menaces de Carabosse

Parce qu’elle n’avait pas été invitée à l’anniversaire des 14 ans de la princesse, la fée Carabosse lance un sort à celle-ci. Elle lui dit : « J’ai numéroté tes six marraines de 2 à 7. Tu dois les placer dans cette figure de façon que la somme des numéros soit 14 dans chacune des trois rangées. Si tu ne réussis pas, tu dormiras pendant 14 ans. »

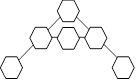
Placez chacune des marraines de façon que la somme des numéros soit 14 dans chaque rangée reliée par une droite.

16. Cœurs de Miguel

Dans la grille ci-dessous, Miguel a dessiné cinq cœurs. Il veut placer trois autres cœurs de façon qu’il y ait deux cœurs dans chaque rangée horizontale et dans chaque rangée verticale.

Disposez trois cœurs.

17. Au restaurant

Quatre amis Aurèle, Barnabé, Carole, Denise se rencontrent au restaurant et dînent à une même table rectangulaire. Deux sont d’un côté et deux de l’autre. Voici une disposition :

Combien y a-t-il d’autres dispositions possibles si Aurèle conserve toujours la même place ?

18. Cavalier de Nathalie

Nathalie prend un cavalier du jeu d’échecs et le promène sur une grille 4 × 5. Le cavalier passe d’une case à l’autre en faisant un L. Il a parcouru les huit premières cases.

Complétez la marche du cavalier pour qu’il atteigne toutes les cases une et une seule fois.

19. Visages colorés

Henri a dessiné des visages dans la grille ci-après. Il a colorié certaines cases.

Coloriez les autres cases en rouge, jaune, gris et bleu de façon qu’il y ait des couleurs différentes dans toute rangée de quatre cases horizontalement, verticalement et diagonalement.

20. Jetons d’Andrée

Andrée découpe neuf jetons et les numérote de 1 à 9. Elle inscrit un nombre dans six cases de la grille.

Complétez la grille avec les neuf jetons pour que la somme soit 20 dans chaque rangée horizontale et verticale.

                                                                                                                                 Solutions 21 à 40

21. Fou de Guildor

Guildor s’amuse à déplacer un fou sur un échiquier. Le fou se déplace obliquement d’une ou de plusieurs cases à la fois. Par exemple, dans cette grille 4 × 4, le fou occupe la case F et domine les trois cases colorées.

Dans une grille 4 × 4, combien de fous sont nécessaires et suffisants pour occuper ou dominer toutes les cases ?

22. Dominos de Rose

Rose prend six dominos : (1, 1), (1, 3), (1, 4), (2, 3), (2, 4) et (3, 4). Elle trace une grille et indique le nombre de points de deux demi-dominos dans deux coins opposés.

Placez les six dominos de façon qu’il y ait 10 points sur chaque côté.

23. Œil de Bruno

Bruno a dessiné trois cercles qui se touchent. Il y a superposé six cellules. Il veut y placer les nombres 1, 3, 4, 5, 6 et 8 de façon que la somme des trois cellules disposées sur chacun des trois cercles soit 12. Le 8 est en bonne position.

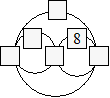
Placez les cinq autres nombres.

24. Cartes de Sara

Sara a dessiné un cœur, un carreau, un pique et un trèfle dans cette grille. Elle veut y placer les autres figures de façon qu’il y ait des figures différentes dans chaque rangée horizontale, verticale et diagonale.

Complétez la grille.

25. Chemins de la fourmi

Une fourmi part de A et veut se rendre à B en suivant les lignes sans jamais revenir en arrière.

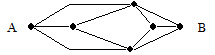
Combien y a-t-il de chemins possibles ?

26. Oméga de Mégane

Mégane dessine la figure ci-après qui est composée de neuf cases pâles. Elle veut y placer les nombres de 2 à 12, sauf 3 et 9. La somme doit être 17 dans chaque rangée de deux ou de trois cases pâles accolées. Le 4 et le 10 sont en bonne position.

Trouvez une façon de distribuer les nombres.

27. Cavalier de Guillaume

Guillaume pousse son cavalier sur la grille ci-après. Le cavalier part de la case 1, va en 2, en 3, en 4 et en 5. Il se déplace toujours en L.  

Combien au minimum le cavalier doit-il parcourir de cases à partir de 5 avant d’atteindre la case noire ? Le cavalier ne peut pas occuper une case déjà atteinte.

28. H de Narcisse

Narcisse veut disposer chaque nombre de 1 à 7 dans les cases de la grille ci-après. La somme doit être 12 dans chacune des rangées de trois cases horizontalement et verticalement, de même que dans les deux diagonales.

Trouvez une façon de distribuer les sept nombres.

29. Fou de Lyne

Lyne déplace un fou dans une grille. Comme aux échecs, le fou se déplace obliquement. Toutefois, le fou de Lyne avance d’un seul pas à la fois. Elle place d'abord le fou dans la case 1, puis dans les cases 2 et 3. Elle a soin de numéroter les cases à mesure qu'elle déplace son fou.

Continuez à déplacer le fou pour qu'il atteigne la case 12. Le fou ne peut pas occuper une case déjà atteinte.

30. Décoration d’un mur

Maude trace une grille 4 × 4 sur un mur de sa chambre. Chaque case est teinte d’une des quatre couleurs : bleu, jaune, rouge ou vert. Chaque case doit recevoir une des quatre figures : ♥, ♣, ●, ■. Les couleurs de trois cases et les figures de trois cases sont données.

Complétez la grille afin de retrouver quatre couleurs et quatre figures différentes dans chaque rangée horizontale, verticale et diagonale.

31. Cases de Victor

Victor a préparé une grille dans laquelle il a écrit 1 et 2 aux endroits indiqués. Il veut maintenant placer les nombres de 3 à 8 pour que la somme soit 14 dans chaque diagonale de trois cases pâles.

Complétez la grille.

32. Simon au gymnase

Simon s’occupe de l’entretien du matériel du gymnase de son école. Lors d’un congé, il vérifie l’état des ballons. Pour ce faire, il dispose les 21 ballons en rangées telles qu’il y a toujours un ballon de plus dans la rangée inférieure.

Disposez les 21 ballons autrement de façon qu’il y ait encore un ballon de plus dans toute rangée inférieure.

33. Marche d’un girafon

Un girafon se promène sur la grille ci-après. En alternance, il fait un saut en L comme le cavalier aux échecs et le saut suivant à la case voisine horizontalement ou verticalement. Voici les quatre premières cases atteintes par le girafon :

Guidez le girafon de façon qu’il passe par toutes les cases, sauf les deux noires, une et une seule fois.

34. Grille d’Alfred

Alfred a préparé une grille 6 × 6. Il y a inscrit des nombres de 1 à 6. Il veut y placer des nombres de 1 à 6 de façon que chaque nombre apparaisse une seule fois dans chaque ligne et dans chaque colonne.

Complétez la grille.

35. Billes de Claudie

Claudie prend neuf billes numérotées de 1 à 9. Elle donne la bille 6 à sa nièce. Dans la figure ci-après, elle place les billes 1 et 2.

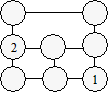
Disposez les six autres billes de façon que la somme des numéros soit 13 dans chaque rangée de deux ou de trois billes reliées par une droite.

36. Fourmi en forme

Laurie pose une fourmi sur la case 1 de la grille. Cette fourmi se déplace en deux mouvements qui se font en alternance. Le premier mouvement est un pas horizontalement ou verticalement. Le deuxième est un pas en diagonale. Un exemple est donné.

Placez la fourmi dans la case du coin supérieur gauche. Trouvez un chemin qui lui permet d’atteindre au moins 12 cases une et une seule fois.

37. Chocolats d’Angèle

Angèle a disposé des chocolats dans une boîte à huit compartiments comme ci-après.

Combien de chocolats doit-on enlever de façon qu’il y en ait sept dans chaque rangée du contour et qu’une case n’en contienne aucun ?

38. Cavalier de Toinette

Toinette pose son cavalier sur la case 1 de la grille ci-après. Comme aux échecs, le cavalier se déplace en L. Les sept premiers sauts sont donnés.

À la suite de 7, trouvez un chemin qui permet au cavalier d’atteindre toutes les cases une et une seule fois.

39. Réunion de proches

Dans une salle, il y a 16 personnes dont les prénoms sont : Alice, Elzéar, Ignace, Octavie. Ce sont quatre Beauvais, quatre Fillion, quatre Jasmin et quatre Perrin. Les 16 personnes se placent en un carré 4 × 4 de façon qu’il y ait ni deux prénoms ni deux noms de famille identiques dans toute rangée horizontale, verticale et diagonale. Cinq personnes sont placées aux bons endroits. Les initiales de leur prénom et de leur nom sont données.

Placez les autres personnes.

40. Cellules de Théo

Théo a dessiné la figure ci-après formée de huit cases pâles. Il veut y disposer chaque nombre de 1 à 9, sauf 4. La somme doit être 16 dans chaque rangée diagonale de trois cases. Théo a déjà placé le 1.

Trouvez une façon de disposer les autres nombres.

                                                                                                                           Solutions 41 à 60

41. Queue de serpent

Julia a écrit 1 dans la case supérieure gauche de la grille 6 × 6 ci-après. Elle continue d’écrire les nombres jusqu’à 20, car il n’est plus possible d’avancer. Seize cases sont vides.

Dans une grille 8 × 8, Julia désire écrire les nombres à partir de 1 en suivant un chemin identique.

Combien de cases seront libres ?

42. Cartes de Mélissa

Mélissa prend neuf cartes : 2, 3, 4 de trèfle, 5, 6, 7 de cœur, 8, 9, 10 de pique. Elle veut les placer en un carré 3 × 3. La somme des nombres de chaque rangée horizontale et verticale est donnée à droite et en bas. Les couleurs (trèfle, cœur, pique) doivent être différentes dans chaque rangée horizontale et verticale. Trois cartes sont en bonne position.

Distribuez les cartes qui manquent.

43. Marche de Fiston

Dans le tracé ci-après, Fiston part de sa maison, soit au point supérieur gauche. Il se déplace sur les lignes. Son école est au point inférieur droit. Fiston a le choix de chemins pour se rendre de la maison à l’école. Le déplacement se fait de gauche à droite et de haut en bas seulement.

Combien y a-t-il de chemins différents pour se rendre de la maison à l’école ?

44. Chemin tortueux

Une tortue part de la case 1. Elle glisse sur une case voisine horizontalement ou verticalement, puis sur une autre case obliquement, toujours en alternance. Les cinq premiers pas de la tortue sont donnés.

À la suite de la case 5, trouvez un chemin que la tortue peut parcourir de façon à atteindre toutes les cases une et une seule fois.

45. Cases de Nathalie

Nathalie a noirci trois cases dans la grille ci-après. En noircissant sept autres cases, elle veut qu’il y ait deux cases noires dans chaque ligne et dans chaque colonne.

Noircissez sept autres cases.

46. Grille de Martin

Martin a préparé une grille dans laquelle on doit écrire des nombres de 1 à 6. Il a donné à droite la somme des deux dernières cases de chaque ligne et en bas celle des deux dernières cases de chaque colonne. Quatre nombres sont déjà en bonne position.

Complétez la grille avec des nombres de 1 à 6 de façon que chaque nombre apparaisse une seule fois dans chaque ligne et dans chaque colonne.

47. Zigzag de René

René dessine la grille ci-après qui est formée de sept cases pâles. Il inscrit d’abord 1 et 3. Dans les autres cases pâles, il désire disposer chacun des nombres de 6 à 10. La somme doit être 18 dans chaque rangée verticale et diagonale.

Distribuez les cinq autres nombres.

48. Chemins de Maude

Maude a écrit les lettres de son prénom dans la figure ci-après. Elle veut lire son prénom en reliant les lettres voisines en diagonale. Elle part du deuxième M.

Combien y a-t-il de façons différentes de lire MAUDE ?

49. Lettres d’Emma

Emma veut placer chacun des nombres de 1 à 10, sauf 7 et 9, dans les cellules du tableau ci-après. La somme des nombres de deux ou de trois cellules reliées par une droite doit être 13. De plus, E + M = 6 et M + A = 8.

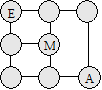
Remplissez le tableau.

50. Cavalier de Miguel

Miguel place un cavalier sur la case 1 de la grille ci-après. Le cavalier, qui se déplace en L comme aux échecs, visite successivement les cases 1, 2, 3, 4 et 5. Par la suite, il ne peut pas occuper une case déjà atteinte.

Trouvez un chemin qui permet de parcourir toutes les cases, sauf celle du milieu.

51. Cartes d’Antoine

Antoine dispose huit cartes de pique en un carré comme ci-dessous. Il forme ainsi quatre rangées de trois cartes de pique chacune.

Placez deux autres cartes de pique de telle manière qu’on retrouve quatre piques dans chaque rangée.

52. Sudoku de Vincent

Vincent a écrit 12 nombres dans cette grille. Il veut écrire des nombres de 1 à 6 de façon que les nombres soient différents dans chaque rangée horizontale, dans chaque rangée verticale et dans chacun des rectangles 2 × 3.

Complétez la grille.

 53. Jetons de Juliette

Juliette dépose six jetons sur la première grille : deux bleus, deux noirs et deux rouges. Un jeton peut être déplacé horizontalement, verticalement ou obliquement en sautant par-dessus un autre.

 Déplacez les jetons de façon à obtenir les positions de cette grille.

54. Boules de Beauvais

Beauvais a composé la figure ci-après dans laquelle il a placé des boules dont le numéro apparaît. Normalement, la somme des numéros de boules en diagonale devait être 22. Étrangement, dans ce cas-ci, aucune diagonale ne présente une somme de 22.

Intervertissez deux couples de nombres pour atteindre une somme de 22 dans chaque rangée de trois cases.

55. Famille Beauregard

Les parents Beauregard sont fiers de leurs neuf enfants. Ils ont écrit trois de leurs prénoms dans la grille ci-après. Les autres enfants sont : Henri, Laurie, Léo, Louis, Sara et Zack.

Trouvez une façon de placer les autres prénoms de façon qu’on puisse compter 15 lettres dans chaque rangée horizontale, verticale et diagonale.

56. Cavalier de Martine

Martine dépose un cavalier du jeu d’échecs sur la case marquée 1. Elle le fait avancer sur la grille en numérotant les sauts. Le cavalier a ainsi parcouru les six premières cases.

Complétez la marche du cavalier pour qu’il atteigne toutes les cases une et une seule fois.

57. Magie de Jérémie

Jérémie trace une grille 3 × 3. Il veut distribuer les nombres 4, 5, 7, 9, 10, 12 et 14 pour que la somme soit 21 dans chaque rangée horizontale, verticale et diagonale de deux ou de trois cases. Le 2 est en bonne position.

Distribuez les nombres.

58. Cases écologiques

Dans cette grille, Lydia a noirci cinq cases. Elle veut colorier sept cases en vert de façon qu’il reste une case blanche dans chaque ligne, colonne et diagonale.

Faites le coloriage.

59. Poussins disparus

Rosanne a acheté 42 poussins. Elle les a placés comme ci-après pour qu’il y en ait 15 par côté de trois enclos. Au bout de deux semaines, elle en retire 6. Elle dispose alors les poussins qui restent pour qu’il y en ait encore 15 par côté et pour qu’ils forment des trios.

Comment les poussins peuvent-ils être répartis ?

60. Cartes de Jonathan

Jonathan prend les neuf cartes suivantes.

Il place les trois cartes 3 dans cette grille.

Placez les six autres cartes de façon qu’il y ait une valeur numérique différente dans chaque ligne et dans chaque colonne et aussi un symbole différent par ligne et par colonne.  

                                                                               Lire la suite