Solution 1. On peut compter 16 carrés 2 × 2.

Solution 2. Louise doit partir du point d’intersection supérieur gauche et terminer au point d’intersection à droite du segment horizontal. On peut le faire dans le sens inverse.

Solution 3. Lise pourrait placer 25 ballons.

Solution 4. Maxime devra utiliser 30 cure-dents.

Solution 5. On compte 16 chemins possibles.

Solution 6. Sofia peut placer 9 dominos.

Solution 7. Il manque 16 petits triangles.

Solution 8. Voici une façon d’assembler les cinq petits carrés :

Solution 9. On peut compter quatre triangles d’une partie, trois triangles de deux parties, deux triangles de cinq parties et un triangle de six parties. En tout, on peut compter 10 triangles.

Solution 10. Un partage est :

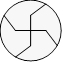
Solution 11. Théoriquement, il y a une infinité de façons de partager une tarte en quatre parties égales. En voici une :

Solution 12. Ludovic a tracé 11 carrés : 8 carrés de quatre châteaux et 3 carrés de neuf châteaux.

Solution 13. On peut obtenir la figure suivante.

Solution 14. Voici un chemin :

Solution 15. On déplace une balle d'un coin vers le centre. On obtient trois petits carrés. Voici un exemple :

Solution 16. Du point supérieur après le C, on compte 7 chemins. Du point central après le C, on compte 5 chemins. Du point inférieur après le C, on compte 7 chemins. En tout, on compte 19 chemins. Le chat perdra le nord.

Solution 17. On prend un des jetons de la rangée verticale, sauf celui à l’intersection des deux rangées, et on le place sur ce dernier.

Solution 18. On peut compter neuf carrés : huit carrés formés d’une seule figure et un carré de trois figures dans le coin supérieur droit.

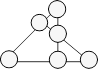
Solution 19. Émerise a planté 21 cerisiers. Il y a un arbre à chaque coin et un arbre au centre des deux diagonales.

Solution 20. On peut disposer les boutons ainsi.

Solution 21. Laura peut construire six rectangles.

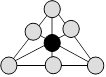
Solution 22. On ajoute au centre le jeton qui est noir.

Solution 23. On compte sept carrés : six de quatre parties et un de neuf parties.

Solution 24. L'abeille parcourt une distance de 85 centimètres.

Solution 25. Chaque partie est représentée par une même lettre.

Solution 26. On peut compter 9 rectangles : quatre rectangles horizontaux de deux pièces, deux rectangles verticaux de deux pièces, un rectangle horizontal de trois pièces, un rectangle vertical de trois pièces et un rectangle de quatre pièces.

Solution 27. On déplace les deux balles placées aux extrémités de la rangée inférieure vers les extrémités de la rangée du centre. On déplace la balle supérieure pour former une nouvelle rangée en bas.

Solution 28. Yasmin plantera 25 roses. Il doit placer une rose à chaque point d’intersection des côtés du pentagone.

Solution 29. On compte 10 triangles : cinq d’une partie, trois de deux parties et deux de trois parties.

Solution 30. On peut compter 18 petits triangles.

Solution 31. On peut placer les jetons ainsi :

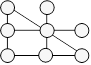
Solution 32. On peut compter sept hexagones dans cette figure.

Solution 33. On peut compter 15 carrés 2 × 2.

Solution 34. Élodie prend 11 jetons de 3 centimètres et 8 jetons de 4 centimètres.

Solution 35. Mira pourra construire six carrés au maximum.

Solution 36. On peut compter six triangles d’une partie, cinq triangles de deux parties et un triangle de quatre parties, soit 12 triangles.

Solution 37. Voici une façon de partager la figure :

Solution 38. En disposant les triangles comme ci-après, il y a le carré formé par la bordure extérieure et le carré intérieur.

Solution 39. Livia peut obtenir 9 points au maximum. Elle peut compléter huit petits carrés et laisser quatre carrés non fermés.

Solution 40. La figure comportera 14 carrés.

Solution 41. On peut compter 10 carrés : huit carrés 2 × 2 et deux carrés 3 × 3.

Solution 42. Tom devra ajouter 15 perles.

Solution 43. Voici les trois autres façons de partager la grille :

Solution 44. On peut glisser vers la gauche la balle qui est au centre de la deuxième colonne. On obtient une rangée horizontale, une rangée verticale et deux rangées diagonales.

Solution 45. Il suffit que la comtesse enlève deux diamants comme, par exemple, le premier et le troisième de la deuxième rangée horizontale. Elle gagnera deux diamants.

Solution 46. On compte 11 triangles : cinq de deux parties, cinq de trois parties et un de six parties.

Solution 47. Réal pourra tracer 13 rectangles.

Solution 48. Chaque partie doit contenir trois carreaux. Voici une façon de partager le potager :

Solution 49. Biche ajoutera six carrés. Il restera deux allumettes qui ne peuvent pas former un carré.

Solution 50. On compte huit rectangles 2 × 3.

Solution 51. On peut compter 48 cases.

Solution 52. On compte 29 carrés : 16 carrés 2 × 2, 9 carrés 3 × 3 et 4 carrés 4 × 4.

Solution 53. Une façon de partager le cadran est :

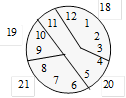
Solution 54. La figure peut être partagée ainsi.

Solution 55. Il faudrait ajouter 20 allumettes.

Solution 56. Par exemple, on accole la cinquième tuile à droite et on l’abaisse comme pour former une marche d’escalier.

Solution 57. Dix cases noires.

Solution 58. Voici une façon de disposer huit T :

Solution 59. Les deux mouches se rencontreront entre le deuxième et le troisième point d’intersection de la droite du haut au tiers pour A et aux deux tiers pour B.

Solution 60. Seul le premier réseau peut être parcouru d’un seul trait.

Solution 61. On peut compter quatre triangles de deux parties et quatre triangles de quatre parties : ce qui fait huit triangles en tout.

Solution 62. Il y avait 28 triangles unitaires dans cette partie.

Solution 63. On compte six triangles dont la base est en bas et six triangles dont la base est en haut. En tout, on peut compter 12 triangles de quatre parties.

Solution 64. Le partage de la figure peut se faire ainsi.

Solution 65. Pour atteindre sa dulcinée, Simon doit d’abord atteindre une des deux roches voisines de A et revenir au point de départ. Voici un chemin de 1 à 17 :

Solution 66. On a 25 kilomètres pour A, 50 kilomètres pour B, 25 kilomètres pour C, 60 kilomètres pour D. Au minimum, les quatre amis devront parcourir 160 kilomètres.

Solution 67. Xénon part du coin supérieur gauche et finit au coin inférieur droit ou inversement.

Solution 68. Il a fallu 12 traits droits.

Solution 69. Une façon de partager le rectangle est :

Solution 70. Voici le triangle :

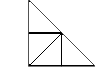
Solution 71. On peut construire cinq petits rectangles.

Solution 72. On peut compter sept triangles d’une partie, trois triangles de deux parties, deux triangles de trois parties, un triangle de sept parties, un triangle de 10 parties. Il y a en tout 14 triangles.

Solution 73. Voici une façon de disposer les pièces :

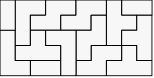
Solution 74. Une façon de procéder est d’enlever le bâtonnet du centre de la première rangée horizontale, puis les deux bâtonnets du coin inférieur gauche.

Solution 75. Les côtés du rectangle mesurent 3 et 12 centimètres. La distance parcourue par la mouche est de 15 centimètres.

Solution 76. On compte 12 triangles d’une partie et quatre triangles de deux parties, soit 16 triangles en tout.

Solution 77. Voici une façon d’agencer les pièces :

Solution 78. Éric parcourt successivement 24 mètres, 36 mètres et 24 mètres, soit un total de 84 mètres.

Solution 79. Voici une façon de former six carrés :

Solution 80. Voici une façon de partager la grille :

Solution 81. La somme des nombres dans chaque partie doit être 30. La grille peut être partagée ainsi :

Solution 82. On peut compter 81 allumettes qui se toucheront en quatre points.

Solution 83. Six points au maximum peuvent coïncider. Voici une façon de disposer les deux triangles :

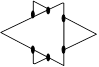
Solution 84. La première crête supérieure de gauche correspond à la moitié de deux carrés, soit l’équivalent d’un carré. La crête suivante correspond à deux demi-carrés soit l’équivalent d’un carré. La crête suivante est l’équivalent d’un demi-carré. La crête de droite correspond à la moitié de quatre carrés, soit l’équivalent de deux carrés. L’ensemble des carrés incomplets équivaut à 4½ carrés.

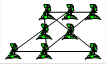
Solution 85. On peut prendre la figurine du centre de la rangée du bas et on la place à la gauche de cette rangée comme ci-dessous.

Solution 86. On peut construire ce pentagone.

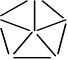
Solution 87. Voici comment on peut partager la figure :

Solution 88. Au total, on peut compter 15 rectangles 2 × 3 qui n’ont pas de cœur.

Solution 89. On dispose les quatre pièces ainsi. Le carré est à l’intérieur.

Solution 90. La grille contient 36 petits carrés.

Solution 91. Voici une façon de partager le terrain :

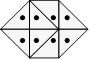
Solution 92. Voici les quatre autres figures :

Solution 93. Neuf traits droits ont été nécessaires : trois traits horizontaux et six traits obliques.

Solution 94. On place un dé sur chacune des cases, sauf celles des coins.

Solution 95. C’est l’amie d’Hilaire qui a raison. On peut tracer cinq croix : quatre croix orthogonalement et une croix obliquement. Voici cette dernière :

Solution 96. Voici une façon de disposer les pièces :

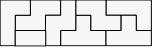
Solution 97. On peut tracer sept carrés. Voici une façon de les tracer :

Solution 98. Antoine aura besoin de 40 allumettes.

Solution 99. On peut compter deux carrés 3 × 3 qui contiennent un carré coloré et deux cercles. Les deux carrés sont sur les 2^e, 3^e et 4^e lignes.

Solution 100. Seule la troisième ne peut pas être tracée.

Solution 101. La capacité d’un moule serait de 36 beignets ; celle de l’autre serait de 72 beignets.

Solution 102. La quatrième figure est :

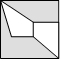
Solution 103. Il devrait y avoir 84 ognons sur la 10^e couronne.

Solution 104. On peut enlever la deuxième allumette de la première rangée verticale, la deuxième allumette de la deuxième rangée horizontale et la troisième allumette de la deuxième rangée verticale.

Solution 105. On peut disposer les dominos ainsi :

Solution 106. On peut obtenir cette figure.

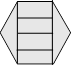
Solution 107. Voici une représentation :

Solution 108. Voici deux façons d’agencer les quatre pièces :

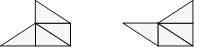
Solution 109. On peut compter 22 rectangles : six 1 × 2 horizontalement, six 1 × 2 verticalement, trois 1 × 3 horizontalement, trois 1 × 3 verticalement, deux 2 × 3 horizontalement, deux 2 × 3 verticalement.

Solution 110. Voici les deux figures :

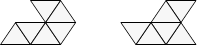
Solution 111. On obtient cette figure.

Solution 112. Méliane peut construire six carrés.

Solution 113. On ajoute au centre la pomme foncée comme ceci.

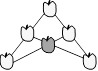
Solution 114. On peut compter six triangles : deux triangles de deux parties, trois triangles de trois parties et un triangle de quatre parties.

Solution 115. Voici une façon de franchir toutes les portes :

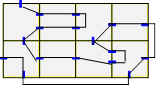
Solution 116. Solange devra prendre 7 rondelles dont la hauteur est de 3 centimètres et 6 rondelles dont la hauteur est de 5 centimètres.

Solution 117. On peut assembler les huit pièces en un carré 6 × 6. Le voici :

Solution 118. Avec trois traits droits, on peut partager le triangle en au plus sept parties. Il faut donc utiliser au moins un trait non droit. Voici une façon de partager le triangle avec deux droites et un cercle :

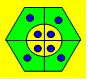
Solution 119. Léa devra parcourir 59 mètres.

Solution 120. Voici une disposition :
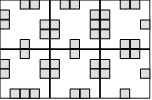