Solution 1. Le numéro du château du milieu est 1003.

Solution 2. Le 12^e nombre trinaire est 1020. Les six autres nombres sont 120, 201, 300, 1002, 1011 et 1020.

Solution 3. Voici une façon de placer les jetons :

Solution 4. La plus grande valeur de §ª est 47.

Solution 5. La figure a 6 côtés.

Solution 6. On prend l’allumette de droite du 6 et on la place avec le 1. On a alors : 3 + 2 = 5. Ou encore, on place cette allumette devant le V pour donner 4. On a alors : 3 + 1 = 4.

Solution 7. Cinq façons différentes : (2, 6), (6, 2), (3, 5), (5, 3), (4, 4).

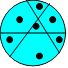
Solution 8. On peut compter 9 triangles : 6 d’une partie, 2 de deux parties et 1 de trois parties.

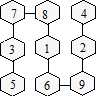
Solution 9. On peut compter 24 droites : 8 horizontalement, 8 verticalement et 8 obliquement.

Solution 10. On peut former 10 groupes de trois pommes : (1, 4, 10), (1, 5, 9), (1, 6, 8), (2, 3, 10), (2, 4, 9), (2, 5, 8), (2, 6, 7), (3, 4, 8), (3, 5, 7) et (4, 5, 6).

Solution 11. Six repas seront nécessaires.

Solution 12. L’objet B pèse 5 grammes.

Solution 13. La dernière rondelle sera rouge.

Solution 14. Le cadenasÏvaut 8 et le Ð vaut 2. La valeur de Ï + Ð est 10.

Solution 15. On peut placer les signes ainsi : 8 ´ 4 + 3 + 5 ´ 6.

Solution 16. Quatre sommes sont possibles : 13, 16, 21, 22.

Solution 17. On peut écrire : 372 + 546 = 918.

Solution 18. On peut compter 22 L.

Solution 19. Voici une disposition possible des pommes :

Solution 20. On peut faire : 7 × 5 = 35, 7 – 5 = 2 et 35 × 2 = 70.

Solution 21. Il y a 6 façons de lire BARBE.

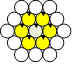
Solution 22. Alexis peut placer 12 oranges dans la deuxième couronne. Voici la disposition des oranges :

Solution 23. Le deuxième dé présente deux fois le 3. Le troisième dé est aussi objet d’erreur car deux faces opposées d’un dé ont 7 points. Les faces 3 ou 4 ne peuvent pas être adjacentes ; elles doivent être opposées.

Solution 24. Arthur a acheté 21 lapins.

Solution 25. Gertrude avait 23 macarons.

Solution 26. L’égalité est : 15 + 26 = 41. La valeur d’ALEXIA est 152641.

Solution 27. A = 78 et B = 42.

Solution 28. À cause de la troisième ligne, il y a 21 boutons par rangée. Les boutons sont disposés ainsi :

Solution 29. Le panier contenait 17 oranges.

Solution 30. Onze traits droits ont été nécessaires.

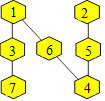
Solution 31. Une configuration est :

Solution 32. La tortue peut emprunter le chemin donné par les lettres en ordre alphabétique.

Solution 33. Myriam a acheté 3 cahiers.

Solution 34. Le plus petit nombre est 247.

Solution 35. Six cases seront coloriées en jaune. Il s’agit d’une grille 6 × 6.

Solution 36. Le code de MULOT est : % u Å o Y.

Solution 37. On peut compter 11 groupes de deux cercles voisins.

Solution 38. Il y a 4 carrés qui contiennent exactement deux cœurs et deux trèfles.

Solution 39. La tirelire contenait 15 florins.

Solution 40. Dans la première rangée, on additionne successivement 2, 4, 6. Pour la cinquième boule, on doit additionner 8 à 17. On obtient 25. Chaque nombre de la deuxième rangée est le double de celui qui lui correspond dans la première rangée. Le numéro de la boule qui devrait suivre dans la deuxième rangée est 50.

Solution 41. Océane doit ajouter 14 crayons.

Solution 42. La distance est de 5 mètres. Pour la calculer, on passe par le premier drapeau.

Solution 43. Un seul trait est nécessaire. Voici le tracé :

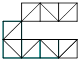
Solution 44. Éva avait 12 cartes. Félix avait 8 cartes. Victoria avait 7 cartes.

Solution 45. On peut lire 15 nombres pairs : 276, 296, 372, 376, 438, 572, 576, 672, 692, 728, 734, 738, 754, 834, 928.

Solution 46. PIE.

Solution 47. La grille remplie est :

Solution 48. On a besoin de 30 trèfles.

Solution 49. VACHE.

Solution 50. La valeur de ▲ est 9. Celle de ♞ est 2. Celle de ♥ est 7.

Solution 51. On peut compter 10 carrés 2 × 2.

Solution 52. Il doit y avoir 7 pommes par rangée : 3 pommes dans le plateau supérieur, puis dans l’ordre 1, 4 et 2 pommes dans les trois autres plateaux. On peut intervertir le 1 et le 2.

Solution 53. Coralie a 28 oranges.

Solution 54. La grille complétée est :

Solution 55. Alicia a 7 timbres et Ludovic en a 13.

Solution 56. Xavier aura besoin de 20 clous.

Solution 57. Le carré magique est :

Solution 58. Zacharie a dépensé 13 pistoles le mercredi.

Solution 59. Il y avait 16 petits triangles.

Solution 60. La grille remplie est :

Solution 61. On remplace le jeton 2 par un jeton 4 et le jeton 9 par l’autre 4. On obtient : 46 + 53 + 34 = 133.

Solution 62. Les deux nombres cherchés sont 22 et 23.

Solution 63. Arthur a 42 ans et Réjeanne, 24 ans. Arthur avait 18 ans quand Réjeanne est née.

Solution 64. On peut compter 14 carrés : 10 carrés 2 × 2 et 4 carrés 3 × 3.

Solution 65. On peut lire RAOUL 9 fois. Raoul a 13 ans.

Solution 66. La plus grande somme est 82. On peut écrire : 35 + 47 = 82 ou 37 + 45 = 82.

Solution 67. Anatole avait 18 pistoles.

Solution 68. Les numéros des bocaux sont 10, 13 et 17.

Solution 69. Les numéros des trois balles sont 6, 7 et 13.

Solution 70. La valeur de A est 3 et celle de B est 26.

Solution 71. Voici une disposition où le (4, 2) est vertical et les deux autres sont horizontaux :

Solution 72. On colorie 11 petits carrés comme ceci.

Solution 73. Treize automobiles.

Solution 74. G = 3, U = 9 et S = 6. La valeur de GUS est 396.

Solution 75. Sophia ne retire aucune automobile. Chaque automobile, en commençant par la dernière peut reculer.

Solution 76. La grille doit être partagée en quatre parties dont la somme est 10. Voici le partage :

Solution 77. L’objet B pèse 3 grammes.

Solution 78. Il faudra 23 allumettes : 16 sur le contour et 7 à l’intérieur.

Solution 79. Victoria avait 24 macarons.

Solution 80. L’amie enlève le segment inférieur de la première rangée verticale. Cela donne 9, le carré de 3.

Solution 81. Le nombre de Sébastien est 64 053.

Solution 82. On place les jetons 3 et 5 au numérateur, puis 2 au dénominateur. On place le 4 avant l’égalité et le 8 après l’égalité.

Solution 83. Alicia possédait 31 florins.

Solution 84. Les cases sont numérotés 5, 13 et 15.

Solution 85. On peut agencer huit rectangles 2 × 3 comme ceci.

Solution 86. Il y a 22 points sur les faces arrière. Sur un dé, deux faces opposées ont une somme de 7 points.

Solution 87. On remplace chacun des deux 7 par 4.

Solution 88. Laurie pourra placer 20 oranges dans la deuxième couronne.

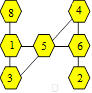
Solution 89. On peut placer les perles ainsi :

Solution 90. Dix pièces seront nécessaires. Il restera quatre petits carrés. Voici un exemple :

Solution 91. Le premier reçoit 15 noisettes, le deuxième 13, le troisième 14.

Solution 92. Patricia a raison. Il suffit de partir d’une extrémité de la droite verticale et de revenir au point de départ.

Solution 93. En tout, on peut compter 15 carrés 3 × 3. Il y a quatre carrés 3 × 3 dans les trois premières lignes, trois dans les lignes 2, 3 et 4, quatre dans les lignes 3, 4 et 5, quatre dans les trois dernières lignes.

Solution 94. Les cinq personnes vont jouer 10 parties.

Solution 95. Les nombres sont 16, 17, 9 et 10.

Solution 96. La plus grande somme est 91. On peut écrire, par exemple, 37 + 54 = 91.

Solution 97. Douze visites ont été effectuées.

Solution 98. SIMON peut être lu 12 fois : six fois en passant par un « i » et six fois en passant par l’autre « i ».

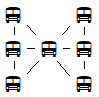
Solution 99. On peut déplacer l’autobus du centre de la rangée du bas vers le milieu comme ceci.

Solution 100. Martin a recueilli 29 étoiles. On peut les disposer ainsi.

Solution 101. De mercredi à vendredi, l’écart est de 6 degrés.

Solution 102. Jean a 9 crayons et Paul en a 7.

Solution 103. Le dernier jour, Laurie a acheté 19 oranges. Elle a acheté successivement 3, 7, 11, 15, 19 oranges.

Solution 104. On peut écrire : (99 − 9 × 9 + 9) ÷ 9 = 3.

Solution 105. La somme des lettres de DINA est 16. D = 6, I = 2, N = 3, A = 5.

Solution 106. Les trois nombres sont 24, 36 et 15.

Solution 107. On peut former 12 nombres pairs de quatre chiffres : six nombres qui se terminent par 4 et six nombres qui se terminent par 6.

Solution 108. On compte 8 points. Ils sont indiqués dans cette figure.

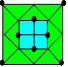
Solution 109. On ajoute les deux étoiles aux extrémités de la rangée horizontale inférieure. Voici la configuration :

Solution 110. Le triangle vaut 6 et le carré vaut 3.

Solution 111. Ils ont 7 et 11 ans.

Solution 112. Le plus petit nombre est 40.

Solution 113. CIEL.

Solution 114. La valeur de y est 6.

Solution 115. La lettre est T.

Solution 116. Voici une façon de distribuer les chiffres :

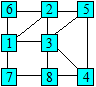
Solution 117. La grille remplie est :

Solution 118. Le numéro est 912 743.

Solution 119. On peut compter six triangles : deux triangles d’une partie, trois triangles de deux parties, un triangle de quatre parties.

Solution 120. Une expression peut être : 3 × 5 × 7 + 10 – 15 = 100.

Solution 121. On compte 18 petits carrés, soit 6 par partie. Le partage de la figure peut se faire ainsi.

Solution 122. Sophia a 5 ans. Livia et Lydia ont 3 ans.

Solution 123. Il y a cinq possibilités de partage : 4 parties de 24 contes, 6 de 16 contes, 8 de 12 contes, 12 de 8 contes et 16 de 6 contes.

Solution 124. Le triangle vaut 5 ; l’hexagone vaut 2.

Solution 125. Les nombres sont 32, 46 et 51.

Solution 126. Une façon de distribuer les nombres est :

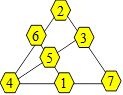
Solution 127. La première boîte contient 48 toutous et l’autre boîte 28 toutous.

Solution 128. La somme des nombres est 39. Les trois sommes partielles doivent être 12, 13 et 14. Le partage peut se faire ainsi :

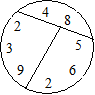
Solution 129. On peut écrire : 33 × 2 + 32 + 2 = 100.

Solution 130. On peut former 6 nombres : 6345, 6354, 6435, 6453, 6534, 6543.

Solution 131. On peut répartir les poussins ainsi.

Solution 132. En tout, elles ont construit 20 cabanes d’oiseaux.

Solution 133. QUATRE-VINGT-QUATORZE.

Solution 134. Le mot est GARAGE.

Solution 135. Marielle peut obtenir 7 parties. Voici un partage :

Solution 136. On ajoute les trois trophées à droite ou à gauche. On a deux rangées horizontales et deux diagonales de trois trophées.

Solution 137. Il y aurait 72 et 54 timbres par album.

Solution 138. On peut écrire : 4 + 5 = 9, 6 ÷ 3 = 2 et 7 + 1 = 8.

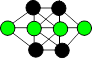
Solution 139. Quatre cercles sont reliés exactement à quatre cercles. Ce sont les quatre cercles noircis.

Solution 140. Il a parcouru successivement 6 mètres, 9 mètres et 27 mètres, soit un total de 42 mètres.

Solution 141. On peut placer les signes ainsi : (4 × 4 – 4) ÷ 3.

Solution 142. Neuf lettres ne seront pas utilisées : B, G, J, K, L, M, V, W et Y.

Solution 143. On peut disposer les autres nombres ainsi.

Solution 144. Cela prendra 6 minutes. Qu’il y ait 6 ou 12 saucisses dans la poêle, c’est le même temps.

Solution 145. On peut former huit nombres : 346, 354, 356, 364, 436, 456, 534, 536.

Solution 146. Il y aura 14 pièces.

Solution 147. On peut compter 6 carrés de quatre cases.

Solution 148. Il y a 12 combinaisons possibles de deux chats.

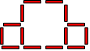
Solution 149. On peut enlever les quatre bâtonnets situés à l’intérieur du grand carré. La nouvelle figure se présente ainsi :

Solution 150. Souriante doit partir de l’intérieur de l’une ou l’autre des pièces triangulaires. Elle doit terminer son chemin au point de départ.

….. FIN …..