Ce recueil touche aux nombres, à l’algèbre, à
la géométrie, aux probabilités et aux statistiques. Il comprend 400 items
dont certains contiennent des questions multiples. On trouve donc plus de
1000 questions.
C’est un excellent moyen de vérifier ses
connaissances dans ces domaines mathématiques. Choisissez les chapitres qui
vous conviennent.
Chapitre 1. Nombres naturels
Chapitre 2. Suites arithmétiques
Chapitre 3. Nombres entiers relatifs
Chapitre 4. Nombres rationnels
Chapitre 5. Rapports et proportions
Chapitre 6. Introduction à l’algèbre
Chapitre 7. Opérations sur les polynômes
Chapitre 8. Équations à une inconnue
Chapitre 9. Équations à deux inconnues
Chapitre 10. Inéquations
Chapitre 11. Notions de base en géométrie
Chapitre 12. Aire et périmètre
Chapitre 13. Repérage dans le plan
Chapitre 14. Solides
Chapitre 15. Probabilités
Chapitre 16. Statistiques
Chapitre
1. Nombres naturels Solutions
1. Calculez mentalement.
a) 65 + 24
b) 72 – 38
c) 56 × 4
d) 168 ÷ 6
2. Vrai ou faux.
a) 161 + 751 = 912
b) 981 – 442 = 439
c) 36 × 27 = 962
d) 964 ÷ 4 = 241
3. Vrai ou faux.
a) La différence de deux nombres est toujours plus
grande que le plus petit nombre.
b) Tout nombre divisible par 3 et par 4 est
divisible par 6.
c) La somme de deux nombres inférieurs à 100 est
toujours inférieur à 200.
d) Un nombre dont la somme des chiffres est 6 est
toujours divisible par 6.
4. Trouvez le nombre qui manque dans chaque case de
la grille.
|
a)
|
|
+
|
15
|
=
|
61
|
|
b)
|
15
|
×
|
|
=
|
210
|
|
c)
|
|
–
|
98
|
=
|
234
|
|
d)
|
|
÷
|
12
|
=
|
76
|
5. Trouvez le terme manquant dans chaque cas.
a) 23 + ■ = 57 ×
2
b) 62 – 18 = ■ ÷ 4
c) 192 + 123 = 63 × ■
d) 648 ÷ ■ = 3 × 27
6. Complétez la grille en faisant les
multiplications.
7. Écrivez une égalité en utilisant les opérations
nécessaires et les nombres donnés dans chaque cas. Le second membre de
l’égalité doit contenir un seul nombre. Par exemple, avec 4, 17, 5, 3,
on peut écrire 4 × 3 + 5 = 17. Trouvez une solution dans chaque cas.
a) 35, 7, 47, 42
b) 25, 5, 2
c) 22, 43, 28, 7
d) 4, 15, 28, 52
8. Complétez les égalités en utilisant des
signes d'opérations et en respectant la priorité des opérations.
a) 5 ... 4 ... 7 ... 3 = 30
b) 7 ... 8 ... 9 ... 2 = 33
c) 12 ... 4 ... 5 = 20 ... 12
d) 15 … 3 … 8 = 16 … 3
9. Remplacez le trèfle par le symbole < ou
>.
a) 7 × 8 ♣ 54
b) 86 + 78 ♣ 150
c) 123 ÷ 3 ♣ 8 × 6
d) 198 – 69 ♣ 200 – 75
10. Sans faire de multiplications, trouvez la somme
des nombres qui devraient apparaître dans la grille lorsqu’on multiplie
les nombres deux à deux.
11. Patrick fête son 18e anniversaire
de naissance pendant lequel il a connu quatre années bissextiles.
Combien de jours Patrick a-t-il vécus ?
12. Un facteur a livré 100 000 lettres en 212
jours.
Combien de lettres le facteur a-t-il livrées en
moyenne par jour ?
13. Alice fait 9 chèques de 18 $ chacun. Il lui
reste 300 $ dans son compte de banque.
Combien Alice avait-elle au début ?
14. Manon achète 12 livres à 19 $ chacun. Il lui
reste 23 $.
Combien d'argent Manon avait-elle avant de faire
ses achats ?
15. Gilles a trois fois moins de macarons que
Sophie. Par ailleurs, Sophie a 48 macarons.
Combien Gilles et Sophie ont-ils de macarons
ensemble ?
16. Danielle gagne 12 $ l’heure. Elle travaille
38 heures dans une semaine. Le montant des déductions à la source est de
85 $.
Quel montant Danielle reçoit-elle pour une semaine
?
17. Marc a un nombre de timbres égal au carré de
15. Marcel a un nombre égal à la racine carrée de 3025.
Combien Marc et Marcel ont-ils de timbres ensemble
?
18. Pour aller à la piscine, Nathalie prend 20
minutes en marchant à une vitesse moyenne de 3 kilomètres à l'heure.
Julie fait le même trajet en 15 minutes.
À quelle vitesse moyenne Julie se déplace-t-elle
?
19. Isabelle possède un nombre de macarons égal
au carré de 17. Josette possède un nombre de macarons égal au carré de
16.
Combien Isabelle a-t-elle de macarons de plus que
Josette ?
20. Michelle a eu 10 points de moins que Julie dans
un examen. Elles ont eu ensemble 150 points.
Quelle est la note de chacune ?
21. Martine a travaillé le mardi 2 heures de plus
que le lundi et le mercredi 3 heures de moins que le lundi. Elle a travaillé
20 heures pendant ces trois jours.
Pendant combien d'heures par jour Martine a-t-elle
travaillé ?
22. Jason a lu un certain nombre de pages dans un
livre. Mario a lu 3 fois plus de pages. Les deux ont parcouru 84 pages.
Combien chacun a-t-il lu de pages ?
23. Jonathan a fait 2 fois moins de longueurs de
piscine que Karine. Ils ont fait ensemble 48 longueurs.
Combien chacun a-t-il fait de longueurs ?
24. Julie a 12 florins de moins que Martin. Ce
dernier a 10 florins de plus que Tristan. Martin et Tristan ont 20 florins
ensemble.
Combien de florins chacun a-t-il ?
25. Deux tomes d’encyclopédie ont ensemble 1000
pages. Le tome 1 a 80 pages de plus que l’autre.
Combien chaque tome a-t-il de pages ?
Chapitre
2. Suites arithmétiques
Solutions
26. Vrai ou faux.
a) Le nombre 164 appartient à la suite des
multiples de 4.
b) La somme de trois nombres impairs consécutifs
est toujours divisible par 3.
c) Le cinquième terme de la suite de nombres pairs
qui commence par 6 est 16.
d) Il y a 50 termes dans la suite des nombres consécutifs
dont le premier terme est 5 et dont le dernier est 55.
27. Trouvez le nombre qui manque.
a) 2, 9, 16, ■, 30
b) 1, 3, 6, ■, 15
c) 2, 6, 12, ■, 30
d) 3, 5, 8, ■, 17
28. Trouvez le cinquième terme d'une suite dont le
premier terme est 2 et dont la différence entre chaque terme est la même.
a) La différence entre chaque terme est 5.
b) La différence entre le deuxième et le troisième
terme est 6.
c) La différence entre le premier et le cinquième
terme est 16.
d) La somme de premier et du cinquième terme est
8.
29. Trouvez le 10e terme de chaque
suite.
a) 4, 8, 12, 16, ...
b) 1, 4, 7, 10, ...
c) 7, 12, 17, 22, ...
d) 9, 15, 21, 27, ...
30. Trouvez le 10e terme d’une suite
dans laquelle chaque terme est égal
a) au double de son rang.
b) au double de son rang augmenté de 7.
c) au triple de son rang diminué de 2.
d) au triple du rang précédent.
31. Trouvez la somme des 10 premiers termes de
chaque suite.
a) 1, 4, 7, 10, 13, …
b) 6, 11, 16, 21, …
c) 45, 42, 39, 36, …
d) 100, 81, 64, 49, …
32. À partir du troisième terme, une suite est
formée par la somme des deux nombres précédents. Trouvez le 6e
terme de cette suite si
a) les deux premiers termes sont 1, 3.
b) les deux premiers termes sont 3, 5.
c) les deux premiers termes sont 5, 7.
d) les deux premiers termes sont 7, 9.
33. Trouvez le nombre de termes dans chaque suite
suivante.
a) 2, 3, 4, 5, 6, …, 87
b) 2, 4, 6, 8, 10, …, 152
c) 2, 4, 7, 11, 16, …, 46
d) 9, 16, 25, 36, …, 225
34. Trouvez le rang d'un terme donné de chaque
suite.
a) 6, 9, 12, 15, ... Le terme est 81.
b) 5, 8, 11, 14, ... Le terme est 101.
c) 2, 7, 12, 17, 22, ... Le terme est 157.
d) 9, 17, 25, 33, ... Le terme est 169.
35. Trouvez la somme des 10 termes d’une suite
a) dont la différence est 5 et dont le premier
terme est 1
b) dont la différence est 6 et dont le dernier
terme est 56
c) dont le premier terme est 10 et dont le dernier
terme est 100
d) dont la différence est 2 et dont le dernier
terme est 22
36. Trouvez la différence entre les termes voisins
d’une suite
a) si le 3e terme est 9 et le 7e
terme est 25.
b) si le 7e terme est 14 et le 11e
terme est 22.
c) si le 4e terme est 15 et le 9e
terme est 35.
d) si le 5e terme est 43 et le 11e
terme est 97.
37. Trouvez la somme du cinquième et du huitième
terme de chaque suite.
a) 4, 7, 10, 13, …
b) 2, 8, 14, 20, …
c) 3, 7, 11, 15, …
d) 10, 12, 14, 16, …
38. La grille ci-dessous doit comporter dans chaque
ligne des suites dont le rang des termes est donné sur la première ligne.
|
2
|
4
|
5
|
7
|
10
|
|
|
23
|
|
|
53
|
|
14
|
|
|
34
|
|
|
|
|
15
|
|
30
|
|
7
|
|
19
|
|
|
Complétez la grille.
39. Trouvez combien la 10e figure
devrait comporter de points noirs.
|
●
● ●
|
● ●
● ● ●
|
● ● ●
● ● ●
●
|
● ● ●
●
● ● ●
● ●
|
40. Chaque terme d’une suite est le triple du
rang, augmenté d’un certain nombre. Le 10e terme de cette
suite est 35.
Quel est le nombre inconnu ?
41. Pour construire une grille carrée 1 × 1, on
doit prendre 4 allumettes. Pour une grille 2 × 2, on a besoin de 12
allumettes. De combien d’allumettes a-t-on besoin pour construire une
grille
a) 3 × 3
b) 4 × 4
c) 5 × 5
d) 10 × 10
42. Pour gravir une montagne, on a construit 10
escaliers. Le premier escalier comporte 7 marches, le deuxième 10 marches,
le troisième 13 marches.
Combien de marches un touriste devra-t-il fouler
pour atteindre le sommet de la montagne ?
43. Pendant 10 jours, la température augmente
successivement d’un degré et baisse de deux degrés le jour suivant. La
température est de 14 degrés le premier jour.
Combien sera-t-elle le dernier jour ?
44. On a besoin de 30 clous pour fixer un premier
panneau, 28 clous pour un deuxième, 26 clous pour un troisième et ainsi de
suite.
Combien de clous seront nécessaires pour fixer le
10e panneau ?
45. La population d’une école augmente de 12 élèves
par année. La 10e année, elle est de 238 élèves.
Combien y avait-il d’élèves la première année
?
46. Le salaire de Roméo augmente de 200 $ par année.
En 2017, il gagnait 32 000 $.
Combien Roméo gagnait-il en 2008 $ ?
47. Au premier arrêt du métro, 12 personnes
embarquent. À chaque nouvel arrêt, 15 personnes y montent et 9 personnes
quittent.
Combien y aura-t-il de personnes dans les wagons à
la suite du 10e arrêt ?
48. Sur le calendrier d’un mois, le 5 mai est un
lundi.
Quel sera le jour de la semaine du 29 juin ?
49. Dans un édifice de 10 étages, les locataires
des 5 derniers étages possèdent ensemble 100 radios. Du premier au 5e
étage, le nombre de radios augmente de 2 d’un étage à l’autre. Du 5e
au 10e étage, le nombre augmente de 3 d’un étage à
l’autre.
Combien y a-t-il de radios au premier étage ?
50. Les quatre plus petits nombres pentagonaux
centrés sont illustrés ci-dessous.
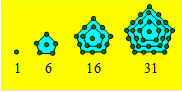
Quel doit être le 10e nombre pentagonal
centré ?
Chapitre
3. Nombres entiers relatifs Solutions
51. Calculez.
a)
(-5 + 7) × (-9 ÷ -3)
b)
-8 + -2 × -5 + 12
c)
63 ÷ -7 + -3 × 12
d)
(-8 × 3) – 9 + 5 × -2
52. Vrai ou faux.
a) La somme de deux entiers de signes contraires
est toujours positive.
b) Le produit de deux entiers négatifs est
toujours positif.
c) La différence de deux entiers dont l'un est 0
est toujours positive.
d) Le quotient d'un entier et de son opposé est
toujours négatif.
53. Trouvez le nombre qui manque dans chaque case
de la grille.
|
a)
|
-5
|
+
|
|
=
|
-2
|
|
b)
|
-7
|
×
|
|
=
|
56
|
|
c)
|
|
–
|
11
|
=
|
-20
|
|
d)
|
|
÷
|
-5
|
=
|
-7
|
54. Complétez la grille en faisant les additions.
55. Trouvez le terme manquant dans chaque cas.
a) -12 + ■ = 23 ×
2
b) 42 – 36 = ■ ÷
-4
c) -36 + 48 = -4 × ■
d) 96 ÷ ■ = 3 × -8
56. Placez les nombres suivants
a) -12, +7, -3, 0, +3 en ordre croissant
b) -7, +4, 0, -2, -3 en ordre décroissant
c) -10, +3, -4, -5, +11 en ordre croissant
d) +8, -8, +3, -3, +5, -5 en ordre décroissant
57. Remplacez le trèfle par < ou >.
a) -2 ♣ -5
b) -8 ♣ 3
c) -5 ♣ (-4 + 4)
d) (-2 × 1) ♣ -7
58. Sans effectuer, indiquez le signe de chaque résultat.
a) -8 + -5
b) (-6)7
c) (-5)3 ÷ -12
d) 23 × (-3)2
59. Vrai ou faux.
a) L'opposé de -4 est 0.
b) La somme de deux entiers négatifs est toujours
négative.
c) Le quotient de deux entiers de signes contraires
est toujours positif.
d) Le produit de deux entiers dont l'un est -1 est
toujours négatif.
60. Calculez les expressions suivantes.
a)
(-5 + 7) ´ (-9
÷ -3)
b)
-8 + -2 ´ (-5
+ 12)
c)
63 ÷ (-7 ´ -3)
+ 12
d)
-8 ´ (3
– 9) + 5 ´ -2
61. Écrivez une égalité en utilisant les opérations
nécessaires et les nombres donnés dans chaque cas. Par exemple, avec -4,
6, -3, lorsque le résultat est -8, on peut écrire -4 × 6 ÷ 3 = -8.
Trouvez une solution dans chaque cas.
a) -5, -4, -2. Le résultat est 18.
b) -3, -2, -1, 4. Le résultat est -15.
c) -8, -3, 6, 7. Le résultat est -58.
d) -12, -10, -4, 8. Le résultat est 30.
62. Écrivez une égalité en utilisant les opérations
nécessaires et les nombres donnés dans chaque cas.
a) 16 avec quatre -2
b) 10 avec quatre -3
c) 8 avec quatre -4
d) -9 avec quatre -5
63. Complétez la grille en faisant les
multiplications.
64. Trouvez le terme manquant dans chaque cas.
a) -30/■ –
5 = -11
b) (28 × -3)/2 = -7 × ■
c) (-32 + 4)/■ + 3 = 10
d) (54 ÷ -3)/■ = 2
65. Sans faire les
multiplications, trouvez la somme des nombres qui devraient apparaître dans
cette grille.
66. Les trois premiers nombres de chaque ligne sont
multipliés pour donner le nombre de droite. Trouvez le nombre qui manque
dans chaque ligne.
|
a)
|
-2
|
+4
|
|
=
|
-96
|
|
b)
|
+8
|
|
-3
|
=
|
-24
|
|
c)
|
-7
|
+3
|
|
=
|
42
|
|
d)
|
+2
|
|
-11
|
=
|
-88
|
67. Le triple d'un nombre augmenté de -14 est égal
à -44.
Quel est ce nombre ?
68. À un moment donné, le thermomètre marque -5
degrés Celsius. Il baisse de 4 degrés, puis monte de 6 degrés.
Quelle est alors la température ?
69. Victoria choisit un nombre. Elle le multiplie
par 2. Elle soustrait -8 au résultat et divise le dernier résultat par -2.
Le résultat final est 16.
Quel est le nombre choisi ?
70. Isaac choisit un nombre. Il est le divise par
-2. Il additionne -8 au résultat et divise le dernier résultat par -7. Le
résultat final est 4.
Quel est le nombre choisi ?
71. Une automobile est équipée pour se mouvoir
aussi facilement d'avant que de reculons. Sur une piste en ligne droite,
elle parcourt successivement +3 kilomètres, -2 kilomètres, +7 kilomètres,
-4 kilomètres et +2 kilomètres.
À quelle distance de son point de départ sera
l'automobile à la fin de sa course ?
72. Dans un building à logements, quel est le
trajet le plus long ?
a) Partir du rez-de-chaussée qui est l'étage 0 et
aller à l'étage +5 ou partir du rez-de-chaussée et aller à l'étage -4.
b) Partir de l'étage -2 et aller à l'étage -6 ou
partir de l'étage -1 et aller à l'étage +4.
c) Partir de l'étage -5 et aller à l'étage +2 ou
partir de l'étage -4 et aller à l'étage +1.
d) Partir de l'étage 0 et aller à l'étage -4 ou
partir de l'étage -1 et aller à l'étage +2.
73. Chloé a trois jetons rouges marquées -2, -3,
-6 et trois jetons verts marqués +4, +5, +7. Elle veut combiner deux jetons
de couleur différente pour que la somme des marques soit 1.
Combien y a-t-il de combinaisons différentes ?
74. Dans la grille ci-après, Alyssa veut placer
les nombres -2, -3, -4, -5, -6 et -7 pour que la somme soit -12 dans chaque
rangée de deux ou de trois cases horizontalement, verticalement et en
diagonale. Le -1 est en bonne position.
Complétez la grille.
75.
Éloi veut placer les nombres -1, -2, -3, -4, -5, -6 dans la grille ci-après
pour que la somme dans chaque rangée horizontale soit -18 et pour que celle
de chaque rangée verticale soit -9. Le -7 et le -8 sont en bonne position.
Trouvez une façon de compléter la grille.
Chapitre
4. Nombres rationnels Solutions
76. Effectuez les opérations suivantes.
a) 2/3 + 5/6
b) -3/2 + 5/8
c) 5/8 ÷ 3/2 + -5/6
d) 5/2 + 1/2 × 9
77.
Calculez.
a) 55 % de 140
b) 72 % de 560
c) 40 % de 0,5
d) 44 % de
10
78.
Calculez.
a) 2/5 de 80
b) 3/4 de 180
c) 2/3 de 69
d) 5/6 de 30
79. Trouvez le nombre qui manque dans chaque cas.
a) 1/3 + ■ = -5/6
b) -2/3 ÷ ■ = 2
c) ■ –
6/7 = 1/14
d) ■ ×
2/3 = -5/3
80. Vrai ou faux.
a) La somme de -4/5
et de 2/5
est 2/5.
b) Le produit de -2/3
et de -3/4
est inférieur à 1.
c) 20 % correspond à 0,2.
d) Le quotient de 4/3 et de 3/4 est 1.
81. Arrondissez chaque nombre à l'ordre de
grandeur donné.
a) 447,8 à l'unité
b) 52,329 au dixième
c) 4,628 au centième
d) 43,6579 au millième
82. Écrivez en chiffres les nombres suivants.
a) deux et dix millièmes
b) quatre et deux centièmes
c) cent quinze millièmes
d) cent trois centièmes
83. Trouvez le nombre qui manque dans chaque ligne
de la grille.
|
a)
|
-2/5
|
+
|
|
=
|
1/10
|
|
b)
|
|
–
|
3/4
|
=
|
7/8
|
|
c)
|
63
|
×
|
|
=
|
-21
|
|
d)
|
|
÷
|
3/2
|
=
|
48
|
84. Placez le symbole < ou > sur les pointillés.
a) 1/3 de -12 .... 1/4 de 20
b) 2/3 de 18 .... 3/4 de -20
c) 70 % de 210 .... 50 % de 180
d) 12 % de 80 .... 15 % de 60
85. Écrivez en fraction ordinaire.
a) 0,4
b) 0,44
c) 1,25
d) 2,53
86. Écrivez en nombre décimal.
a) 1/5
b) 3/8
c) 7/16
d) 9/25
87. Écrivez en pourcentage.
a) 5/8
b) 3/7
c) 0,78
d) 1,234
88. Effectuez les opérations suivantes.
a) 45,6 – 18,4 + 12,7
b) 39,92 + 0,04 – 4,567
c) 52,4 + 23,56 – 18,453
d) 76,843 – 29,6 + 13,477
89. Effectuez les multiplications suivantes.
a) 7,2 ´
6
b) 0,005 ´
78
c) 2,25 ´
48
d) 83 ´
0,45
90. Effectuez les divisions suivantes.
a) 4,56 ¸
100
b) 3,05 ¸
1000
c) 2,34 ¸
4
d) 5,681 ¸
3
91. Dans la grille ci-après, Alyssa veut placer
les nombres 1/2, 1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2 pour que la somme soit 7 1/2
dans chaque rangée horizontale, verticale et diagonale. Les nombres 1 et 2
sont placés.
Complétez la grille.
92. Renée achète 2 livres à 13,75 $ le livre.
Elle achète des menus objets pour 10,50 $. Il lui reste 2 $.
Quel était le montant d’argent de Renée ?
93. Martin a travaillé 22 heures à 8,95 $ de
l'heure. Les déductions sur sa paie sont de 28 %.
Quel montant Martin a-t-il reçu ?
94. Dans une école qui accueille 250 enfants, 1/10
des enfants portent des lunettes. De ce nombre, 3/5 sont des garçons.
Combien de garçons portent des lunettes ?
95. Gilles possède une collection de 243 macarons.
Il donne les 2/9 de sa collection à son frère. Puis, il vend les 4/9 de ce
qui lui reste.
Combien Gilles a-t-il de macarons maintenant ?
96. Rolande a entrepris de lire un roman de 240
pages. Elle a lu 80 % du roman.
Combien de pages lui reste-t-il à lire ?
97. Alain dépense le tiers de son argent, puis le
quart de ce qui reste. Il donne 6 florins à son frère. Il lui reste encore
6 florins.
Combien de florins avait-il au début ?
98. Paul part de Rimouski pour se rendre à Québec.
La distance entre les deux villes est de 310 kilomètres. Il parcourt les
2/5 de cette distance et s’arrête au restaurant.
Quelle distance lui reste-t-il à parcourir ?
99. Julie a peint le quart d’une perche en rouge,
le tiers en bleu. Il lui reste à peindre la dernière partie en vert.
Quelle fraction de la perche lui reste-t-il à
peindre ?
100. Dans la grille ci-après, Alyssa veut placer
les nombres 0,25 ; 0,5 ; 0,75 ; 1 ; 1,25 ; 1,5 ; 1,75 ; 2 ; 2,25 pour que la
somme soit 3,75 dans chaque rangée horizontale, verticale et diagonale.
Trois nombres sont placés aux bons endroits.
Complétez la grille.
Chapitre
5. Rapports et proportions Solutions
101. Trouvez le terme manquant dans chaque
expression.
a) 3/8 = 12/n
b) n/6
= 7/1,5
c) 25/4 = n/
0,2
d) 14/n
= 3,5/6,5
102. Indiquez par oui ou par non si chacun des
rapports forme une proportion.
a) 5/2 et 4/10
b) 8/3 et 24/9
c) 25/36 et 5/6
d) 3 : 5 et 10 : 6
103. Vrai ou faux.
a) Un des rapports équivalents à 4/5 est 20/25.
b) 16/25 est équivalent à 4/5.
c) 0,2/5 est équivalent à 1/25.
d) Dans 5/6 = 10/12, 10 est un moyen terme.
104. Partagez le nombre proportionnellement dans
les rapports donnés.
a) 48 dans le rapport 1 à 2
b) 540 dans le rapport 4 à 5
c) 600 dans les rapports 2, 3 et 5
d) 630 dans les rapports 1, 3 et 5
105. Agencez les nombres suivants pour former une
proportion, le plus petit nombre étant le numérateur d’une fraction.
a) 3, 6, 7, 14
b) 11, 10, 2, 55
c) 120, 20, 30, 5
d) 4, 25, 20, 5
106. Trouvez le rapport entre les deux nombres.
a) 24 et 84
b) 17 et 340
c) 21 et 49
d) 64 et 204
107. Dans les situations suivantes, établissez le
rapport sous forme d’une fraction en respectant l’ordre des données.
a) Cynthia étudie 12 heures par semaine tandis que
Marc étudie 8 heures par semaine.
b) Un cahier mesure 30 centimètres de longueur par
18 centimètres de largueur.
c) Martin donne 750 $ à l’aînée et 550 $ au
cadet.
d) Marcelle cueille 30 paniers de pommes pendant
que Julien cueille 28 paniers.
108. Partagez
a) 260 $ dans le rapport 5 à 8
b) 33 heures dans le rapport 3 à 8
c) 136 kilomètres dans le rapport 12 à 5
d) 196 points dans le rapport 11 à 3
109. Le rapport de deux nombres est de 7 à 3. Le
plus petit nombre est 36.
Quel est l’autre ?
110. Une somme d’argent est
composée de deux parties qui sont dans le rapport 3 à 7. La plus grande
somme est 147 $.
Quelle est la plus petite
somme ?
111. Le nombre d’oranges de
deux paniers est dans le rapport 5 est à 6. Il y a 125 oranges dans le plus
petit panier.
Combien les deux paniers
contiennent-ils d’oranges en tout ?
112. L'équipe des Bleus a compté 15 points en 7
parties. L'équipe des Jaunes, pour sa part, a compté 20 points en 9
parties.
Quelle équipe a le plus performé ?
113. Cynthia suit 4 heures de cours de mathématiques
sur 30 heures. De son côté, Marc suit 5 heures sur 33 heures.
Qui, proportionnellement, consacre le plus de temps
aux cours de mathématiques ?
114. Annie a payé 4,65 $ pour 5 canettes de jus
marqués à un même prix. De son côté, Éric a payé 10,56 $ pour 12
canettes marqués à un autre même prix.
Qui a payé ses canettes au prix le plus élevé ?
115. Jean-Claude et Patricia partent en voyage.
Jean-Claude conduit pendant 2,5 heures et parcourt 210 kilomètres. Patricia
conduit pendant 1,5 heure à la même vitesse moyenne.
Combien de kilomètres Patricia a-t-elle parcouru
en conduisant ?
116. Dans un magasin d'alimentation, on vend 3 boîtes
de céréales au blé entier pendant qu'on vend 7 boîtes de céréales au
raisin. En une semaine, 102 boîtes au blé entier ont été vendues.
Combien de boîtes de ces céréales ont été
vendues au total pendant ce temps ?
117. Dans un magasin de vêtements, il y a 7 employés.
Ils ont vendu pour 6748 $. La patronne pense que si elle engageait 2 employés
de plus, la vente moyenne de chaque employé serait la même.
Quelle serait alors la vente totale ?
118. Une pancarte mesure 60 centimètres de
longueur sur 36 centimètres de largeur. Après réduction proportionnelle,
sa largeur est de 9 centimètres.
Quelle est la longueur de la pancarte réduite ?
119. Martin achète 7 livres au coût de 67,20 $.
Martine achète 3 livres ayant le même coût moyen.
Combien Martine paiera-t-elle pour ses 3 livres ?
120. Sonia a payé 49,95 $ pour 5 disques compacts
de même prix. Yves achète 9 disques au même prix par disque.
Combien Yves paiera-t-il au total pour ses achats ?
121. Dans un magasin de sports, on vend 7 paires de
ski pendant qu'on vend 3 paires de raquettes. Au cours de l'année, la vente
de raquettes s'est élevée à 126 paires.
Combien de paires de ski ont été vendues ?
122. Gilles a parcouru 20 kilomètres en 3 heures
à bicyclette. À la même vitesse moyenne, Nadine fait une randonnée de 2
heures.
Combien Nadine a-t-elle parcouru de kilomètres ?
123. Un marché d'alimentation vend 12 boîtes de céréales
au coût de 26,88 $. Alain a 16,50 $ dans son porte-monnaie.
Combien pourra-t-il acheter de boîtes de céréales
au maximum ?
124. Claude cueille 4 épis de blé de maïs
pendant que Josée en cueille 5. À la fin de la journée, Josée en a
cueilli 635.
Combien Claude et Josée ont-ils cueillis d'épis ?
125. Catherine a payé 8,45 $ pour 5 cahiers marqués
à un même prix. De son côté, Paul a payé 6,88 $ pour 4 cahiers marqués
à un autre même prix.
Qui a payé ses cahiers au coût le moins élevé ?
Chapitre
6. Introduction à l’algèbre
Solutions
126. Attribuez à chaque proposition un des mots
suivants : degré, coefficient, terme, variable.
a) Comment appelle-t-on 5 dans 5a2b ?
b) Comment appelle-t-on x
dans 10x2y
?
c) Comment appelle-t-on 8mn
?
d) Comment appelle-t-on 2 dans 7a2b ?
127. Indiquez s’il s’agit d’un monôme,
d’un binôme ou d’un trinôme.
a) 5x –
3y + 6
b) x2
– 9
c) 7x2
d) 4xy +
3x2
128. Vrai ou faux.
a) Dans 4ab2,
a et b sont des termes.
b) Dans 3ab4, 4 est appelé constante.
c) Une expression algébrique qui contient
plusieurs termes est un polynôme.
d) 3ab et
3ab2 sont des termes
semblables.
129. Trouvez la valeur de chaque polynôme si a
= -2 et b = 3.
a) 5b
b) -4a
c) 2a + b
d) 7a –
8b
130. Trouvez le nombre qui manque si x = -2.
a) 3x2
+ ■
= 9
b) 5x –
4 = ■
c) -2x2
+ ■
= x
d) ■ + 3x = 5x
131. Trouvez le terme qui manque dans chaque case
de la grille.
|
a)
|
4x
|
+
|
-3x
|
=
|
|
|
b)
|
2x
|
×
|
5x
|
=
|
|
|
c)
|
|
–
|
3x
|
=
|
9x
|
|
d)
|
8x
|
÷
|
|
=
|
4
|
132. Trouvez la valeur de x.
a) 3x =
18
b) 5x2
= 20
c) 2x + 3x
= 35
d) 8 – 4x = 12
133. Trouvez la valeur de y.
a) 3y + 5y
– 6y = 12
b) y + 20
– 2y = 23
c) 8y –
6y = 3y
– 10
d) 12 + 4y
= 5y + 3
134. Complétez la grille en faisant les additions.
135. Complétez la grille en faisant les
multiplications.
136. Placez le symbole < = ou > au lieu du trèfle.
a) -3x ♣
8x – 5x, si x = 2
b) 2y + 5
♣
15, si y = -4
c) 3z –
7z ♣
-2z – 2z,
si z = -3
d) 5x –
8 ♣
12 – 3x, si x = 3
137. Remplissez la grille avec des nombres pour que
la somme de chaque rangée, horizontale et diagonale soit 42.
138. Complétez la grille en remplaçant chaque
expression par leur valeur numérique.
|
a
|
b
|
a2 – b
|
2a
– b2
|
|
-2
|
3
|
|
|
|
0
|
-5
|
|
|
|
3
|
-1
|
|
|
139. Mario a travaillé (5z
– 2) heures. Pierrette a travaillé (2z
– 3) heures.
Pendant combien d'heures Mario et Pierrette ont-ils
travaillé en tout ?
140. Pierre a acheté (a
+ b2) albums de bandes
dessinées. On sait que a est égal
à -3 et que b est égal à 4.
Combien Pierre a-t-il acheté d'albums ?
141. Vous prenez deux nombres. Le plus petit nombre
est a. Le deuxième est égal au
premier augmenté de 5.
Quelle est la somme de ces deux nombres ?
142. Patrick a joué (7y
– 3) parties de billard. Mélanie a joué (5y
– 2) parties.
Combien Patrick et Mélanie ont-ils joué de
parties de billard ?
143. Pierre-Luc a acheté (m2 – n)
calculatrices. On sait que m est
égal à -3 et que n est égal à
-2.
Combien Pierre-Luc a-t-il acheté de calculatrices
?
144. Guylaine a choisi deux nombres. Le plus petit
nombre est x. Le deuxième est le
suivant en ordre croissant.
Quelle est la somme de ces deux nombres ?
145. Maryse a reçu (x
– 5) livres en cadeau. Elle a lu (x
– 7) de ces livres.
Combien de livres lui reste-t-il à lire ?
146. Alain a fait un voyage qui a duré (2p2
– q) jours. On sait que p
est égal à -3 et que q est égal
à -5.
Combien de jours a duré le voyage d'Alain ?
147. Maria choisit deux nombres. Le plus grand
nombre est b. Le deuxième est égal
au premier diminué de 3.
Quelle est la différence entre ces deux nombres ?
148. David a gagné (7a
– 2) médailles aux sports. Natacha a gagné (5a – 3) médailles.
Combien David a-t-il gagné de médailles de plus
que Natacha ?
149. Dans une semaine, Yves a gagné (b + 5) dollars. Il a dépensé (b
– 2) dollars.
Combien lui reste-t-il ?
150. Julie a acheté (x
– 3) oranges. Elle en a mangé (x
– 7).
Combien d'oranges lui reste-t-il ?
Chapitre
7. Opérations sur les polynômes Solutions
151. Complétez.
a) La somme de 5x,
3x + 2 et 6y est …
b) La différence de 8x
– 3 et de 6x + 9 est …
c) Le produit de 3x
– 2 et de 5x est …
d) Le quotient de 8x
– 12 et de 4 est …
152. Trouvez la valeur numérique de chacune des
expressions si a =1, b = -2 et c = 0.
a)
3a + b2 + c
b)
ab – c3
+ 2b
c)
a2 – b + 2ab
d) a2b
+ bc – ac
153. Vrai ou faux.
a) Le produit de a
et de b est (a + b).
b) Si je multiplie 3x
et 2y, j'obtiens 5xy.
c) Si je divise 14a
par 7, j'obtiens 7a.
d) Le quotient de -2a3
par -2a2 est a.
154. Trouvez le terme qui manque.
a) 2x(x
+ 3) = ■
+ 6x
b) 8y –
3(5y – 1) = ■
+ 3
c) 4(x
– 4) + ■
= 7x – 16
d) 3y +
5(y – ■)
= 8y – 10
155. Additionnez les expressions suivantes.
a)
(4x2 – 5) + (-3x2
+ 4)
b)
(-6a + 3b) + (2a – 5b)
c)
(3m2 – 5ab)
+ (-4m2 – 3ab)
d) (8a + b3
– c) + (-5a – b3
+ c)
156. Soustrayez les expressions suivantes.
a)
(-5a + 3b) – (8a – 3b)
b)
(2a2 + 5ab)
– (-3a2 – 4ab)
c)
(5x2 – 3xy)
– (7xy – x2)
d)
(2a3 + 3ab
– 5) – (7a3 – 3)
157. Effectuez les multiplications suivantes.
a) 5ab ×
-3a
b)
-7p2 × - pq
c)
-3a/4 × -80/3
d)
-ay/2 × -4ay2/6
158. Effectuez les multiplications suivantes.
a) -2(3x
– 5y)
b) 3a2(a
– b – 2a3)
c) -5m(m2
– 3m + 1)
d) 2x(-x
– y – x2)
159. Effectuez les divisions suivantes.
a) 15a2
÷ 5x
b) 21a2x2
÷ -3ax2
c) 12x2y
÷ 6xy2
d) -3a2b
÷ -ab
160. Effectuez les divisions suivantes.
a)
(8a2 – 16) ÷ 4
b)
(3a2y – 15ay) ÷ -3a
c)
(15a2 – 35a3)
÷ a2
d) (12x2y
– 36xy3) ÷ 3xy
161. Vrai ou faux.
a) Si je divise -12x2
par -4x, j'obtiens 3x.
b) Si je multiplie 2a
et -5b, j'obtiens (-10a
+ b).
c) Le quotient de 15x
et de 3x est 5x.
d) Le produit de x
et de -y est (x – y).
162. Effectuez.
a)
(3x - 5)(x + 2)
b)
(2x – 7)(2x + 3)
c)
(3a – b)(3a – b)
d) (a2
+ 2a + 1)(a – 2)
163. Cinq copains ont résolu chacun (a – 7) problèmes.
Combien les cinq copains ont-ils résolu de problèmes
au total ?
164. Sylvain consacre y
minutes par jour aux sports.
Trouvez le nombre de minutes que Sylvain consacre
aux sports pendant (x + 2) jours.
165. Jean-Luc a (x2
– 5x) pièces de monnaie. Il
veut les répartir également en x
personnes.
Combien chaque personne recevra-t-elle de pièces
de monnaie ?
166. Françoise parcourt (3b + 2) kilomètres par jour.
Combien Françoise parcourra-t-elle de kilomètres
pendant (b – 3) jours ?
167. Brenda vend (a
+ 3) macarons par jour.
Combien vendra-t-elle de macarons en une semaine ?
168. Un annuaire téléphonique contient (3x
– 2) noms par page.
Combien y a-t-il de noms si l'annuaire contient y
pages ?
169. Jason a réussi 2z2
examens en z mois.
Combien Jason a-t-il réussi d'examens en moyenne
par mois ?
170. Éric lave (y
+ 5) vitres par logement.
Combien Éric lavera-t-il de vitres dans (y
– 2) logements ?
171. Guillaume a transporté 4a2 passagers en a
voyages.
Combien de passagers Guillaume a-t-il transporté
en moyenne par voyage ?
172. Mathieu a vendu (a
– 3) chapeaux en moyenne par client. Il a eu (a + 5) clients.
Trouvez le nombre de chapeaux vendus par Mathieu.
173. Jennifer lave (a
– 2) automobiles par semaine.
Combien d'autos Jennifer lavera-t-elle en quatre
semaines ?
174. Christiane achète 2x
cartes de hockey à chacun de ses amis. Christiane se vante d’avoir (x
– 3) amis.
Trouvez le nombre de cartes achetées par
Christiane.
175. Remplissez la grille avec des nombres pour que
la somme de chaque rangée, horizontale et diagonale soit 39, lorsque a
= 3 et b = 2.
|
3a
+ 5b
|
a + b
|
|
|
6b
– a
|
|
|
|
3a
+ b
|
|
|
Chapitre
8. Équations à une inconnue
Solutions
176.
Vrai ou faux.
a) (3x
– 5) est une équation.
b) Pour avoir une équation, il faut un signe =.
c) x = 4
est une équation équivalente à 2x
= 8.
d) Si j'additionne 5 à 3a,
je puis écrire (3a + 5).
177. En langage courant, on peut exprimer (5 ¸
3) comme étant le quotient de 5 et de
3. Exprimez en langage courant.
a) 9 ´
3
b) 9 + -7
c) 52 – 8
d) 7 – 3 ´
8
178. En langage mathématique, on peut exprimer le
quotient de 5 et de 3 par 5 ¸
3 ou 5/3. Exprimez en langage mathématique.
a) La moitié de 9.
b) Le double de 5 augmenté de 8.
c) La somme de 5 et de -12.
d) Le tiers de 7 diminué de 4.
179. Pour chaque proposition, choisissez les
nombres qui conviennent dans l'ensemble : í2,
3, 5, 7, 10, 12, 15, 23, 35ý.
a) x est
un entier supérieur à 12.
b) x est
divisible par 3.
c) x est
plus petit ou égal à 7.
d) x est
un multiple de 2.
180. Trouvez la valeur de la variable dans chaque
cas.
a) 5y –
2 = 33
b) 2x –
5 = -9
c) x/3
– 8 = 11
d) 5a + a
– 3 = 21
181. Dans chaque cas, on donne à n les valeurs successives de 1 à 5. Quelle sera la suite ?
a) 3n + 2
b) 4n –
1
c) 2n + 3
d) 5n –
4
182. Dans chaque cas, on donne à n les valeurs successives de -5, -4, -3, -2, -1. Quelle sera la
suite ?
a) 2n + 7
b) -n + 8
c) 3n +
10
d) -2n +
5
183. Traduisez chaque proposition en une équation
en prenant x comme variable.
a) La somme d’un nombre et de son quadruple est
35.
b) La différence d’un nombre et de sa moitié
est 42.
c) Le produit d’un nombre et de son double est
18.
d) Le quotient d’un nombre au carré et de son
quart est 20.
184. Dans chacune des équations suivantes, trouvez
la valeur de A.
a)
B + A = 12
b)
A – x = 15
c)
2A + y = 18
d)
A + 19 = B + 21
185. Traduisez chaque proposition en une équation
en prenant x comme valeur du
nombre.
a) En additionnant 52 à un nombre, on obtient 85.
b) Huit fois un nombre, diminué de 3, est égal à
3 fois ce nombre.
c) Le quart d'un nombre, augmenté de 5, est égal
à 35.
d) En retranchant 5 à un nombre, on obtient un résultat
égal au double de ce nombre.
186. Deux équations sont équivalentes quand elles
ont la même solution. Les équations suivantes sont-elles équivalentes ? Répondez
par oui ou non.
a) 2x + 6
= 10 et 6x + 18 = 30
b) 3x + 1
= 7 et x + 1 = 3
c) 5x –
2 = 13 et 3x + 1 = 13
d) x – x/2
= 12 et x – 18 = 6
187. Trouvez le terme manquant dans chaque cas.
a) 5x –
■
= 8 si x = 3
b) 3x + ■
= 13 si x = -2
c) 4x + 8
= ■
si x = -1
d) x/2 + ■
= 13 si x = 10
188. On peut représenter la suite 1, 3, 5, 7, 9,
… par (2n – 1) où n est le rang du terme. Représentez les suites suivantes.
a) 1, 4, 7, 10, 13, …
b) 2, 4, 6, 8, 10, …
c) 3, 7, 11, 15, 19, …
d) 4, 5, 6, 7, 8, …
189. Trouvez le cinquième terme de la suite qui
est représentée par
a) 3n + 2
b) 2n + 3
c) 4n –
2
d) n + 5
190. Francine a (y
– 6) ans.
Quel âge aura-t-elle dans 10 ans ?
191. Isabelle et Renée ont ensemble x dollars. Isabelle a 5 dollars.
Quel est l'avoir de Renée ?
192. Martin achète deux gilets qu'il paie x
dollars chacun et une casquette qu'il paie 7 dollars.
Quel est le coût de ses achats ?
193. Mélanie achète 12 cahiers. Elle remplit x
cahiers par mois pendant 3 mois.
Combien Mélanie a-t-elle de cahiers non remplis au
bout de trois mois ?
194. Lucie achète x
pommes. Michel commande deux fois plus de pommes. Mais, il lui en manque 5.
Combien Michel a-t-il de pommes ?
195. Michel et Julie ont 35 ans ensemble. Michel a
3 ans de plus que Julie.
Quel est l'âge de Michel ?
196. Une libraire vend un certain nombre de livres.
Le triple de ce nombre augmenté de 8 est égal à 41.
Combien la libraire a-t-elle vendu de livres ?
197. Julie partage 150 dollars entre Yves et
Myriam. Yves doit recevoir 12 dollars de moins que Myriam.
Quel montant Myriam obtiendra-t-elle ?
198. Le double de l'âge de Nathalie, augmenté de
8, est égal à 52 ans.
Quel est l'âge de Nathalie ?
199. Un marchand a vendu 84 boîtes de céréales
en deux jours. Le second jour, il a vendu 4 boîtes de plus que le premier
jour.
Combien de boîtes de céréales ont été vendues
le premier jour ?
200. Pierre et Paul ont ensemble 24 dollars. Pierre
a 10 dollars de moins que Paul.
Quel montant Paul possède-t-il ?
Chapitre
9. Équations à deux inconnues
Solutions
201. Vrai ou faux.
a) 2x + 3y = 34 est une équation
à deux inconnues.
b) Dans l’équation, x
+ 3y = 15, si y
vaut 3, x vaut 5.
c) Dans l’équation 2x
– y = 9, si x
est impair, y est pair.
d) Dans l’équation 3x
– 4y = 16, si x
est pair, y peut être pair.
202. Quelle est la valeur de l’expression (3x
– y) ?
a) Si x =
1 et y = 4
b) Si x =
4 et y = -2
c) Si x =
-3 et y = 10
d) Si x =
-4 et y = 0
203. Trouvez deux nombres dont la somme est 20 et
dont
a) la différence est 10
b) le produit est 99
c) le quotient est 9
d) les deux sont des carrés
204. Trouvez deux nombres dont la différence est
12 et dont
a) la somme est 18
b) le produit est 28
c) le quotient est 3
d) l’un est le quadruple de l’autre
205, Trouvez deux nombres dont le produit est 48 et
dont
a) la somme est 14
b) la différence est 22
c) le quotient est 3
d) l’un est impair
206. Trouvez deux nombres dont le quotient est 3 et
dont
a) la somme est 20
b) la différence est 16
c) le produit est 75
d) les chiffres sont 1, 2, 3 et 6
207. Complétez la grille en faisant les additions
lorsque x = 1 et y = 5.
208. Complétez la grille en faisant les
multiplications lorsque x = -2 et y
= 3.
209. Trouvez la valeur de (x + y) lorsque
a) x + 3
= 12 et y – 5 = 15
b) 2x =
-8 et y + 5 = 12
c) –x +
10 = x et -2y = -8
d) -2x =
24 et 3y = 36
210. Dans les équations suivantes, trouvez la
valeur de x lorsque y = 5.
a) 3x –
6y = 12
b) 5x + 3y
= 25
c) -x + 4y
= -10
d) x/2
– 5y = 0
211. Trouvez la valeur de x par rapport à y.
a) 3x –
2y = 15
b) –x +
4y = 16
c) 5x –
7 = y
d) x/2
– 2y = 9
212. Paul et Jeanne ont ensemble 40 macarons. Paul
a trois fois plus de macarons que Jeanne. On considère x comme le nombre de macarons de Paul et y le nombre de macarons de Jeanne.
Écrivez les deux équations.
213. Deux fois le nombre de paires d’espadrilles
de Marie plus trois fois le nombre de paires d’espadrille de Clara est 31.
Marie a trois paires d’espadrilles de plus que Clara. On considère x comme le nombre de paires d’espadrilles de Marie et y
le nombre d’espadrilles de Clara.
Écrivez les deux équations.
214. Une municipalité est composée de 740
personnes. Il y a 10 femmes de plus que d’hommes. On considère x comme le nombre d’hommes et y
le nombre de femmes.
Écrivez les deux équations.
215. Guillaume a payé 50 $ pour deux jouets. Le
premier jouet a coûté 6 dollars de moins que l’autre. On considère x comme le coût du premier jouet de et y celui du deuxième jouet.
Écrivez les deux équations.
216. Jonathan partage 25 dollars entre ses deux
amis. L'un a 3 dollars de plus que l'autre.
Quels montants ont les deux amis ?
217. Éric et Patricia ont cueilli en tout 74
contenants de fraises. Il manquait un contenant à Patricia pour avoir le
double de contenants d'Éric.
Combien Éric a-t-il de contenants ?
218. Valérie et Olivier ont vendu 177 billets de
tirage en tout. Si Olivier avait vendu 7 billets de plus, il en aurait eu le
triple de Valérie.
Combien Valérie a-t-elle vendu de billets ?
219. L'âge de Jason est le double de celui de
Mathieu. Jason et Mathieu ont ensemble 36 ans.
Trouvez l'âge de chacun.
220. Julie connaît trois nombres dont la somme est
87. Le deuxième est égal à deux fois le premier et le troisième est supérieur
de 3 au premier.
Quels sont ces trois nombres ?
221. Andrée et Patricia ont acheté en tout 85
macarons. Patricia en a acheté le double, augmenté de 7.
Combien chacun a-t-il acheté de macarons ?
222. Mathieu et Hélène ont joué en tout 35
parties de hockey. Il manque 4 parties à Mathieu pour avoir le double d'Hélène.
Combien Mathieu a-t-il joué de parties ?
223. Dans un examen de mathématiques, Georges a eu
5 points de plus que Christiane. Les deux ont eu ensemble 173 points.
Quelle est la note de chacun ?
224. Myriam connaît deux nombres dont la somme est
78. L'un des nombres est supérieur de 14 à l'autre.
Quel est le plus petit nombre ?
225. Françoise et Germain ont ensemble 1215
timbres. Germain en a trois fois plus, diminué de 5, que Françoise.
Combien chacun a-t-il de timbres ?
Chapitre
10. Inéquations Solutions
226. Vrai ou faux.
a) 2x ñ
-8 est une inéquation.
b) x peut
prendre la valeur 4 dans 2x – 7 á
3.
c) x peut
prendre la valeur 0 dans x ñ
0.
d) Le symbole £
signifie plus petit ou égal.
227. Pour chaque cas, dans l'ensemble í0,
1, 3, 5, 7, 9, 10, 15, 17ý,
choisissez les nombres qui conviennent.
a) 3a
< 12
b) 5a + 3
> 48
c) 7a –
8 £
27
d) 8a –
84 ³
-4
228. Traduisez chaque proposition par une équation
ou une inéquation en prenant x
comme variable.
a) En additionnant 17 à un nombre, on obtient 36.
b)
En additionnant 8 à un nombre, on obtient un résultat supérieur au double
de ce nombre.
c) Trois fois un nombre, diminué de 7, est égal
à 4 fois ce nombre.
d)
La moitié d'un nombre, diminuée de 8, est plus grande que 29.
229. Indiquez par oui ou par non si le nombre 8
peut être une solution de chaque inéquation.
a) 2x >
8
b) -2x >
12
c) 3x + 5
≤ x
d) x + 12
< 3x
230. Résoudre les inéquations suivantes.
a)
2x >
4 – x
b)
-2x >
-16
c)
3x + 20 ≤ x
d)
x + 12 < 10 – x
231. Vrai ou faux lorsque x = 4.
a) 3x >
-4
b) -2x >
10
c) 3x + 7
≤ x
d) x + 9
< 10 + x
232. Trouvez les multiples de 10 entre 0 et 55 qui
vérifient les inéquations suivantes.
a) 2x >
40
b) -2x >
-60
c) 3x +
50 ≤ x
d) x –
100 < 8 – x
233. Dans les inéquations suivantes, trouvez les
valeurs de x sous forme d’une inéquation
lorsque y = -4.
a) 3x –
2y >
12
b) -x + 5y
< 15
c)
3x + y
≤ x
d) 2x –
14 < 8 – y
234. Placez le symbole < ou > dans chaque
case lorsque x = 2 et y = -3 en lisant de gauche à droite.
235. Traduisez chaque proposition en une inéquation
en prenant x comme variable.
a) La somme d’un nombre et de son quadruple est
plus grand que 35.
b) La différence d’un nombre et de sa moitié
est plus petit que 42.
c) Le produit d’un nombre et de son double est
plus grand ou égal à 18.
d) Le quotient d’un nombre au carré et de son
quart est plus petit ou égal à 20.
236. Vrai ou faux.
a)
Si j'additionne 2 à chacun des membres de 3x
– 5 < 8, j'obtiens 5x – 3
< 10.
b)
Si je soustrais 5 à chacun des membres de 2x
+ 3 > 11, j'obtiens 3x – 2
< 6.
c)
Si je multiplie par 3 chacun des membres de 2x
– 1 < 5, j'obtiens 6x + 3
< 15.
d)
Si je divise par 2 chacun des membres de 6x
– 8 > 12, j'obtiens 3x – 4
> 6.
237. Julie et Mélanie ont ensemble moins de 42
dollars. Mélanie a 5 dollars de plus que Julie.
Quel est, en dollars, le montant le plus élevé
que peut posséder Mélanie ?
238. Yvan achète deux cadeaux à un coût inférieur
à 75 dollars. Le second coûte 15 dollars de plus que le premier.
Quel est, en dollars, le coût maximal du premier
cadeau ?
239. Mario et Julie ont gagné ensemble moins de
400 dollars au cours du dernier mois. Julie a gagné 60 dollars de plus que
Mario.
Quel est, en dollars, le montant maximal gagné par
Julie ?
240. Mélanie a x
macarons. Elle en reçoit deux fois plus qu'elle en a. Puis, elle en reçoit
10. Son nombre de macarons est supérieur ou égal à 190.
Traduisez cette situation par une inéquation.
241. Martin collectionne les petites autos. S'il reçoit
15 autos en cadeau, il en aura plus de 160.
Combien Martin peut-il avoir d'autos au minimum ?
242. Nicolas travaille à temps partiel dans un dépanneur.
« Si le patron double mes heures et m’attribue en surplus 3 heures,
je travaillerai 25 heures ou moins par semaine, dit-il à un de ses amis ».
Pendant combien d'heures par semaine Nicolas
travaille-t-il au maximum ?
243. Natacha a un sac de balles de golf. Si on enlève
12 balles dans le sac, ce dernier contiendra plus de 40 balles.
Combien de balles le sac peut-il contenir au
minimum ?
244. Louise a regardé x
films en janvier et deux fois plus en février, puis 7 en mars. Pendant ces
trois mois, elle a regardé 64 films ou moins.
Combien de films au maximum Louise a-t-elle regardé
en janvier?
245. Jacinthe achète x
cahiers de jeux. Quelques semaines après, elle en achète trois fois plus.
Puis finalement, elle achète 12 autres cahiers. Jacinthe possède alors
plus de 64 cahiers de jeux.
Traduisez cette situation par une inéquation.
246. Marie-Jeanne aime beaucoup les romans
policiers. Après avoir reçu 7 romans en cadeau, elle en a plus de 45.
Combien Marie-Jeanne pouvait-elle avoir de romans
policiers au minimum ?
247. Valérie compose 3 poèmes qui totalisent 84
lignes ou moins. Le premier poème contient deux fois plus de lignes que le
second. Le troisième a 12 lignes.
Combien de lignes le second poème peut-il contenir
au maximum ?
248. Lucie a vendu moins de 75 billets de tirage en
2 mois. Le second mois, elle a vendu deux fois plus de billets que le
premier mois.
Combien Lucie peut-elle avoir vendu de billets au
maximum le premier mois ?
249. Roméo a vendu plus de 125 drapeaux dans deux
boutiques. Dans la boutique A, il en a vendu 15 de moins que dans la
boutique B.
Combien Roméo peut-il avoir vendu de drapeaux au
minimum dans la boutique B ?
250. Pendant deux semaines, Benoît a passé 37
heures ou moins devant la télévision. La première semaine, il a passé 5
heures de plus que la seconde semaine.
Combien d'heures au maximum Benoît peut-il avoir
passé devant la télévision pendant la seconde semaine ?
Chapitre
11. Notions de base en géométrie Solutions
251. Vrai ou faux.
a) Une droite est limitée par deux points.
b) Dans le plan, la droite est le plus court chemin entre deux points.
c) Par deux points donnés, on peut faire passer plusieurs droites.
d) Deux droites ne peuvent se couper qu’en un seul point.
252. Comment appelle-t-on ?
a) Une droite qui en coupe une autre à angles
droits
b) Deux droites qui ne se coupent pas
c) Une droite limitée par un seul point
d) Une droite limitée par deux points
253. Vrai ou faux.
a) La bissectrice d’un angle partage l’angle en
deux angles de même mesure.
b) Un angle aigu peut mesurer 92 degrés.
c) Un angle obtus peut mesurer 150 degrés.
d) Un angle plat mesure 360 degrés.
254.
Donnez le nom du triangle.
a) Il n'a
aucun côté congru.
b) Il a
2 angles de 45°.
c) Il a 3
angles de 60°.
d)
Il a 2 côtés congrus.
255.
Complétez.
a) Un triangle qui a deux angles de 40° est un triangle
...
b) Un triangle qui a un angle de 40° et un de 50° est un triangle
...
c) Un triangle qui a au moins deux angles de 60° est un triangle
...
d)
Un triangle qui a un angle droit est un triangle ...
256.
Dans un triangle, comment appelle-t-on
a)
le côté opposé à un sommet donné
b)
une perpendiculaire qui joint un sommet et la base correspondante
c) la droite qui joint un sommet et le milieu de la
base correspondante
d)
une perpendiculaire élevée au milieu d’un côté d’un triangle
257. Dans chaque cas, donnez le nom du quadrilatère.
a) Il a seulement deux côtés parallèles.
b)
Il n'a pas d'angle droit. Ses côtés opposés sont parallèles deux à deux
et congrus deux à deux.
c) Il a quatre côtés congrus et des diagonales
non congrus.
d)
Il a des côtés congrus deux à deux et au moins un angle de 90°.
258. Vrai ou faux.
a) Un carré a au moins trois angles droits.
b) Les côtés opposés d’un carré sont parallèles
deux à deux.
c) Les diagonales d’un carré se coupent en leur
milieu.
d) Les diagonales d'un carré se coupent à angles
droits.
259. Vrai ou faux.
a)
Les diagonales d'un rectangle se coupent à angles droits.
b)
Les côtés opposés d’un rectangle sont parallèles
deux à deux.
c) Si on accole deux carrés égaux côté par côté,
on obtient un rectangle.
d) Les diagonales d’un rectangle se coupent en
leur milieu.
260. Vrai ou faux.
a) Les côtés opposés d'un parallélogramme sont
congrus.
b)
Les angles à la base d'un parallélogramme sont congrus.
c) Les diagonales d’un parallélogramme se
coupent en leur milieu.
d) Les côtés opposés d'un parallélogramme sont
congrus.
261. Vrai ou faux.
a) Les angles d'un trapèze isocèle sont tous
congrus.
b)
Le trapèze peut avoir trois côtés congrus.
c)
Les côtés opposés d'un trapèze sont congrus.
d)
Les diagonales d'un trapèze isocèle sont congrus.
262.
Vrai ou faux.
a)
Un losange peut avoir un angle droit.
b)
Un losange a au moins deux côtés parallèles.
c)
Les diagonales d’un losange se coupent à angles droits.
d)
Les angles opposés d’un losange ont la même mesure.
263. Indiquez par oui ou par non si chacune des
figures suivantes peut avoir au moins un angle droit.
a) un losange
b) un triangle rectangle
c) un trapèze
d) un triangle équilatéral
264. Combien y a-t-il de paires de segments parallèles
dans
a) un carré
b) un losange
c) un parallélogramme
d) un trapèze rectangle
265. Combien y a-t-il de côtés congrus dans
a) un carré
b) un losange
c) un parallélogramme
d) un rectangle
266. Combien peut-on compter de diagonales dans
a) un triangle
b) un quadrilatère
c) un pentagone
d) un hexagone
267. Comment appelle-t-on
a) un polygone à 3 côtés
b) un polygone à 4 côtés
c) un polygone à 5 côtés
d) un polygone à 6 côtés
268. Comment appelle-t-on
a) un polygone à 7 côtés
b) un polygone à 8 côtés
c) un polygone à 10 côtés
d) un polygone à 12 côtés
269. Quelle est la somme des angles intérieurs
d’un
a) triangle scalène
b) triangle rectangle
c) losange
d) pentagone régulier
270. Soit la figure suivante.
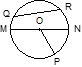
Vrai ou faux.
a) ON est un rayon.
b) QM est une corde.
c) NP est un arc.
d) NOP est un angle au centre.
271. Vrai ou faux.
a) Une sécante est une droite qui coupe le cercle
en deux points.
b) Un arc est une portion de disque.
c) Un angle au centre de 90° détermine un arc de
45°.
d) Tous les rayons d'un même cercle sont
congrus.
272. Complétez.
a)
La longueur du cercle est appelée ...
b)
Un angle dont le sommet est le centre du cercle est appelé ...
c)
Une portion de cercle est appelée ...
d) La plus longue corde du cercle est appelée ...
273. Dans chaque cas, indiquez si les figures sont
toujours, jamais ou parfois semblables.
a) deux cercles
b) deux losanges
c) deux triangles
d) un carré et un cercle de même aire
274.
Vrai ou faux.
a)
Lorsqu'on fait un déplacement autour d'un point, on effectue une réflexion.
b)
Lorsqu'on fait une rotation, les mesures d'angles augmentent ou diminuent de
valeur.
c)
Une translation ne modifie pas une figure.
d)
Une rotation est un déplacement autour d'un point.
275.
La figure de gauche H a subi deux transformations successives.
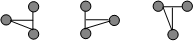
H
a
b
Identifiez
chacune de ces transformations.
Chapitre
12. Aire et périmètre Solutions
276. Indiquez s'il s'agit du périmètre ou de
l'aire dans chacune des situations suivantes.
a) Le contour du dessus d'une table
b) La surface d'une piscine
c) La longueur d'une clôture qui entoure un
terrain
d) La superficie d'une ville
277. Calculez le périmètre.
a) Un carré dont un côté mesure 4 centimètres
b) Un rectangle dont la base mesure 5 centimètres
et dont un autre côté est le triple
c) Un losange dont un côté mesure 6 centimètres
d) Un triangle rectangle dont les deux côtés de
l’angle droit mesurent 3 et 4 centimètres
278. Calculez l’aire.
a) Un carré dont un côté mesure 4 centimètres
b) Un rectangle dont la base mesure 2 centimètres
et dont un autre côté est le triple
c) Un losange dont les diagonales mesurent 6 centimètres
et 5 centimètres
d) Un triangle rectangle dont les deux côtés de
l’angle droit mesurent 3 et 4 centimètres
279. Trouvez la circonférence d'un cercle.
a) si le rayon mesure 8 centimètres.
b) si le diamètre mesure 100 centimètres.
c) si un angle de 60° forme un arc de 12 centimètres
sur la circonférence.
d) si un angle de 45° forme un arc de 15 centimètres
sur la circonférence.
280. Soit le polygone suivant.
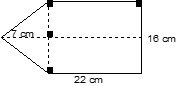
Trouvez l’aire.
281. Soit le polygone suivant.
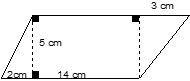
Trouvez l’aire.
282. Josée découpe une pièce de bois ayant la
forme d'un triangle rectangle. Les deux côtés de l'angle droit mesurent
respectivement 36 centimètres et 54 centimètres.
Trouvez la superficie de la pièce de bois.
283. Un plancher de forme rectangulaire mesure 4 mètres
sur 6 mètres. Un tapis occupe un espace carré de 3 mètres de côté.
Quelle est la superficie du plancher qui n'est pas
recouverte par un tapis ?
284.
Jeanne découpe une pièce de tissu en forme de parallélogramme. La base
mesure 15 centimètres et la hauteur, 12 centimètres. Elle plie la pièce
sur sa diagonale.
Quelle
sera l’aire de chaque morceau ?
285. Les côtés parallèles d'un trapèze mesurent
respectivement 5 et 8 centimètres. La distance qui les sépare est de 3
centimètres.
Trouvez l'aire du trapèze.
286. Jeannot achète un terrain de forme
rectangulaire. Un des côtés mesure 80 mètres et le périmètre est de 260
mètres.
Quelle est la superficie du terrain ?
287. Un calendrier de forme rectangulaire occupe
une superficie de 300 centimètres carrés. L'un des côtés mesure 60
centimètres.
Quelle est la mesure des trois autres côtés ?
288. Un mur mesure 2 mètres sur 5 mètres. Mélanie
y a placé une pièce décorative en forme de losange dont les deux
diagonales mesurent respectivement 1 mètre sur 2 mètres.
Quelle est l'aire de la partie restante ?
289. La base d'un parallélogramme mesure 14 centimètres
et la hauteur 18 centimètres. Éric dessine un carré de 8 centimètres de
côté à l'intérieur du parallélogramme.
Quelle est l'aire de la partie restante ?
290. Martin a fabriqué une pièce décorative en
forme de triangle rectangle. Un des côtés de l'angle droit du triangle
mesure 75 centimètres et l'aire est de 600 centimètres carrés.
Quelle est la mesure de l'autre côté de l'angle
droit ?
291. Julien découpe une bande de tissu en forme de
losange. La distance entre les sommets opposés 2 à 2 est respectivement de
17 et 24 centimètres.
Quelle est l'aire de la bande de tissu ?
292. Daniel partage une pizza. Chaque pointe mesure
10 centimètres de côté et a un angle au centre de 45°.
Quelle est la mesure de la surface de chaque pointe
?
293. Michel découpe, dans du carton, un cercle
dont le diamètre mesure 10 centimètres. Il trace deux rayons qui forment
un angle de 30° et découpe cette partie.
Quelle est l'aire de la partie découpée ?
294.
Un panneau rectangulaire mesure 6 mètres sur 10 mètres. On veut construire
un panneau plus petit de même forme dont le coefficient de proportionnalité
est 3/4 pour chaque côté.
Quelle
est la superficie du nouveau panneau ?
295.
Jonathan possède un terrain rectangulaire qui mesure 30 mètres de largeur
et 35 mètres de longueur. Il tend une corde d'un coin du terrain à l'autre
coin opposé.
Quelle
est la longueur de la corde ?
296.
Anne découpe un panneau triangulaire ayant un angle droit. Les côtés de
l'angle droit mesurent 50 et 120 centimètres.
Quelle
est la mesure du troisième côté ?
297.
Michèle et Julie partent du même endroit et marchent en ligne droite.
L'une va vers le sud et l'autre vers l'est. Chacune marche trois kilomètres.
À
quelle distance sont-elles l'une de l'autre à ce moment ?
298.
Andrée place une échelle de 13 mètres qui atteint le haut d'un garage de
12 mètres de hauteur.
À
quelle distance du bas du garage se trouve le pied de l'échelle ?
299.
Un câble d'acier qui mesure 12 mètres est attaché par un bout au sommet
d'un poteau et par l'autre bout à une tige plantée en terre. La tige est
à 3 mètres du poteau.
Quelle
est la longueur du poteau ?
300.
Patrick possède deux tiges. L'une mesure 7 centimètres et l'autre 24
centimètres. Il place les deux tiges de façon à former un angle droit.
Trouvez
la longueur d'une troisième tige qui permettra de former un triangle.
Chapitre
13. Repérage dans le plan Solutions
301. Dans le plan cartésien, comment appelle-t-on
a) Le point (0, 0)
b) L’axe des x
c) L’axe des y
d) Chacune des quatre régions
302. Vrai ou faux.
a) Les deux droites appelées axes sont parallèles.
b) Pour désigner un point, on place l’abscisse
en premier et l’ordonnée en second.
c) Une droite parallèle à l’axe des x est perpendiculaire à l’axe des y.
d) Une droite perpendiculaire à l’axe des y
coupe l’axe des x en un point.
303. Indiquez dans quel quadrant se trouvent les
points
a) (2, 3)
b) (-5, 4)
c) (4, -3)
d) (-3, -1)
304. Dans le plan cartésien, identifiez le lieu de
chaque sommet du triangle MNP.
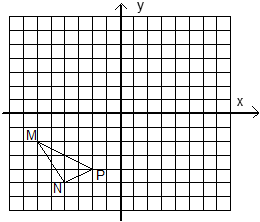
a) M
b) N
c) P
305. Déterminez le quadrant dans lequel se
trouvent les coordonnées de signes suivants.
a) (-, +)
b) (-, -)
c) (+. +)
d) (+, -)
306. Indiquez la position occupée par chaque
dessin dans la grille suivante.
|
K
|
|
|
©
|
|
|
|
J
|
|
|
|
¨
|
|
|
H
|
|
§
|
|
|
|
|
G
|
|
|
|
|
ª
|
|
F
|
|
|
|
|
|
|
|
A
|
B
|
C
|
D
|
E
|
a) §
b) ¨
c) ©
d) ª
307. Karl a écrit
les lettres de son prénom dans la grille suivante : K en (C, 4), A en
(F, 4) et R en (B, 1). Indiquez la position de la lettre L pour avoir un
parallélogramme.
308. Dans le plan cartésien, une mouche se place
sur le point milieu de (-5, 6) et de (-5, -2) et termine sa marche sur le
symétrique du point milieu par rapport à l’axe des y.
Quel point la mouche va-t-elle atteindre ?
309. Vrai ou faux
a) Le symétrique
de (-5, -2) par rapport à (-5, 2) est (-5, 0).
b) Le symétrique
de (-3, 3) par rapport à l’origine est (3, -3).
c) Le point milieu
de (5, -2) et (-5, 3) est (0, 0).
d) Le point milieu
de (1,-5) et (-5, 1) est (5, 1).
310. Un marcheur part du centre de la case (C, J),
passe par le centre de (E, H), de (D, F) et de (B, G) pour atteindre son
point de départ.
Quel est le nom de la figure formée ?
311. Soit le point (-3, 5), trouvez le point qui
est symétrique par rapport
a) à l’axe des abscisses
b) à l’axe des ordonnées
c) à l’origine
d) au point (-3, 1)
312. Un segment de droite est délimité par (2,
-6) et (8, -6). On trace une perpendiculaire sur le milieu du segment.
Par quel point passe la perpendiculaire ?
313. Un mobile part du point (-4, 3) et s’arrête
au point (2, 3). Un autre mobile se déplace sur le segment symétrique du
premier par rapport à l’axe des x.
Déterminez les points qui délimitent le dernier
segment ?
314. Un mobile part du point (1, 3). Il passe par
(1, -3) et (4, -3).
Quelle est la distance parcourue ?
315. Un mobile part du point (-2, -4) et passe par
l’origine.
Quel point atteindra-t-il quand il aura parcouru la
même distance à partir de l’origine ?
316. En suivant les lignes du plan, on trace un
carré. L’un des sommets est le point (3, 5) et un autre est (3, -4).
À quels points vers la gauche les autres sommets
seront-ils ?
317. On déplace
le triangle MNP dans le quadrant I. Deux des sommets sont (2, 4) et (4, 1).
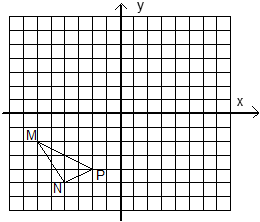
Quel est le troisième
sommet ?
318. Dans un plan cartésien, on relie les points
(0, 0), (3,0) et (0, -4).
Quel est le périmètre de la figure ainsi formée
?
319. Un côté
d’un carré est délimité par les points (-3, 5) et (-3, -1).
Quelle est
l’aire du carré ?
320. Les sommets d’un triangle rectangle sont les
points (2, -3), (2, 3) et (-6, 3).
Trouvez la mesure de l’hypoténuse du triangle.
321. À partir du point (3, -3), on trace une
droite qui finit au point (-1, 1).
Quelle est l’aire du carré dont ce segment est
une diagonale ?
322. On situe les points (3, -4) et (-7, -4) dans
un plan cartésien.
Combien y a-t-il de points du plan cartésien entre
les deux ?
323. Trouvez le point d’intersection de l’axe
des x et d’une droite dont deux
points sont (3, 4) et (-3, -4).
324. On trace un quadrilatère dont les points sont
: (-2, 3), (-1, 5), (-4, 5) et (-5, 3).
Comment appelle-t-on ce quadrilatère ?
325. Dans le plan
cartésien, on situe les points (2, 4), (-3, 4), (-3, 1), (0, 1), (-3, -2).
On relie les points par deux segments horizontaux et un segment vertical
passant par trois points.
Quelle lettre
peut-on former ?
Chapitre
14. Solides
Solutions
326. Je suis une forme géométrique à trois
dimensions. Je suis formé de deux classes : les corps ronds et les
polyèdres.
Choisissez la bonne réponse : volume, solide,
polygone, cylindre.
327. Je suis une forme géométrique à trois
dimensions qui comporte au moins une surface courbe. Un cornet de crème
glacée est de cette forme. Le globe terrestre l’est aussi.
Choisissez la bonne réponse : polyèdre,
volume, corps rond, sphère.
328. Je suis une forme géométrique à trois
dimensions. Mes faces sont planes. Elles sont formées de polygones de différentes
classes.
Choisissez la bonne réponse : polyèdre, sphère,
hexagone, volume.
329. Dans un solide, je suis une surface plane fermée
qui s’emboîtent les unes aux autres. Je peux être formé par des
polygones ou par des cercles. Sur le dé, des points y apparaissent.
Choisissez la bonne réponse : arête, polyèdre,
aire, face.
330. Dans un solide, je suis la ligne d’intersection
de surfaces planes ou courbes, comme des segments de droite ou des segments
de courbes. Par exemple sur un dé, je suis à la limite de deux faces.
Choisissez la bonne réponse : bissectrice, arête,
parallèle, aire.
331. Dans un solide, je suis le point d’intersection
de deux ou de plusieurs arêtes. Par exemple, sur un dé, je suis chacun des
coins.
Choisissez la bonne réponse : origine, médiatrice,
sommet, médiane.
332. Je suis un solide formé à partir d’un
cercle. J’ai deux faces : une courbe et une plane. J’ai un seul
sommet.
Choisissez la bonne réponse : cylindre, cône,
pyramide, prisme.
333. Je suis un solide muni d’une base
polygonale. Mes faces latérales sont des triangles. Chacun des coins du
polygone de la base est relié au sommet par un segment de droite appelé arête.
Choisissez la bonne réponse : cylindre, cône,
pyramide, sphère.
334. Je suis un solide ayant une seule face courbe.
Je suis souvent associé à une boule.
Choisissez la bonne réponse : sphère, cône,
pyramide, prisme.
335. Je suis un solide qui possède une face courbe
et deux faces parallèles. Ces deux dernières faces sont planes et
circulaires. Je suis associé aux boîtes de pois verts.
Choisissez la bonne réponse : cylindre, cône,
pyramide, sphère.
336. Je suis un solide dont les six faces sont
planes et carrées. On m’appelle aussi hexaèdre régulier. J’ai 12 arêtes
toutes de même longueur et 8 sommets.
Choisissez la bonne réponse : cylindre, cône,
pyramide, cube.
337. Je suis un solide qui a deux faces parallèles
appelées bases. Mes sommets sont joints deux à deux par des arêtes qui délimitent
les faces latérales.
Choisissez la bonne réponse : cylindre,
prisme, pyramide, cube.
338. Je suis la mesure de la place occupée par un
corps dans l’espace.
Choisissez la bonne réponse : aire, périmètre,
volume, superficie.
339. Dans un solide, je suis la somme des aires des
faces autres que les bases.
Choisissez la bonne réponse : aire des
sommets, aire latérale, aire totale, surface.
340. Dans un solide, je suis la somme de l’aire
latérale et des aires des bases.
Choisissez la bonne réponse : aire des
sommets, aire latérale, aire totale, surface.
341. Vrai ou faux.
a) Le prisme oblique est un polyèdre.
b) Les faces latérales d'un prisme pentagonal sont
des pentagones.
c) La base d'une pyramide est un polygone
quelconque.
d) Un prisme triangulaire est constitué de quatre
triangles.
342. Pour chaque solide, indiquez le nombre total
de faces.
a) Le cube
b) Le cylindre
c) La sphère
d) La pyramide à base carrée
343. Déterminez l'unité à privilégier pour
mesurer chacun des volumes suivants.
a) Le contenu d'une bouteille de lait
b) Un ballon de soccer
c) Une maison
d) L'eau d'une piscine
344. Un prisme triangulaire droit mesure 20 centimètres
de hauteur. Chaque base est un triangle rectangle dont les côtés de
l'angle droit mesurent respectivement 3 et 4 centimètres et l'hypoténuse 5
centimètres.
a) Trouvez l'aire d'une base.
b) Trouvez l'aire latérale.
c) Trouvez l'aire totale.
345. Une canette a 12 centimètres de hauteur.
Le rayon de la base mesure 3 centimètres.
a) Trouvez l'aire d'une base.
b) Trouvez l'aire latérale.
c) Trouvez l'aire totale.
346. Michelle construit un dé cubique en carton.
Chaque arête mesure 8 centimètres.
Trouvez l'aire du carton qu'elle a utilisé.
347. Une orange de forme sphérique a un rayon de 4
centimètres.
a) Trouvez l'aire de l'orange.
b) Trouvez le volume de l’orange.
348. Mario moule son sucre d'érable dans des
contenants en forme de brique. La base du contenant mesure 15 centimètres
sur 8 centimètres. Sa hauteur est de 6 centimètres.
Quelle est l'aire totale d'un contenant ?
349. Julie a acheté un cornet vide qui contient
normalement de la crème glacée. Le rayon de la base mesure 4 centimètres
et la hauteur est de 15 centimètres.
Quelle quantité de crème glacée le cornet
peut-il contenir ?
350. Martin a cueilli 12 000 centimètres cubes de
fraises. Il les répartit dans des récipients d'un demi-litre.
Combien Martin aura-t-il de récipients pleins ?
Chapitre
15. Probabilités Solutions
351. Vrai ou faux.
a) Le lancement d'un dé est une expérience aléatoire.
b) La probabilité d'un événement peut être supérieure
à 1.
c) En jetant une pièce de monnaie, on a le même
nombre de chances de sortir pile et face.
d) La probabilité de tirer une voyelle du mot EAU
est égale à 1.
352. Carl écrit les nombres de 1 à 25. Trouvez le
nombre de cas favorables où Carl choisit au hasard
a) un nombre pair
b) un nombre impair plus petit que 10
c) un multiple de 3
d) un nombre pair plus grand que 24
353. Dans le jeu classique de 52 cartes, trouvez la
probabilité de tirer
a) une carte rouge
b) un carte de trèfle
c) un carte qui contient une figure (roi, dame,
valet)
d) une carte rouge ou une carte noire
354. Maélie lance un dé sur la table. Trouvez la
probabilité d’avoir sur la face supérieure
a) 5 points
b) un nombre de points inférieur à 4
c) un nombre pair de points
d) un nombre de points supérieur à 6.
355. Zoé a placé dans une boîte 2 billes
blanches, 3 billes vertes et 4 billes jaunes. Trouvez la probabilité de
tirer
a) une bille jaune
b) une bille verte
c) une bille blanche ou une bille jaune
d) une bille blanche et une bille jaune
356. Dans une boîte, Lucie placez les lettres du
mot MATHÉMATIQUES. Trouvez le nombre de cas favorables quand on tire
a) un M
b) un U
c) une voyelle
d) une consonne
357. Danny a placé dans un sac 3 jetons rouges
marqués 1, 2 et 3. Il place dans un autre sac 3 jetons bleus marqués 1, 2
et 3. Il sort en même temps un jeton rouge et un jeton bleu et il fait la
somme des numéros. Énumérez les résultats possibles lorsque la somme est
a) 1
b) 3
c) 4
d) 5
358. Les 8 prénoms suivants Bernard, Caroline,
David, Éric, Bernard, Julie, Caroline, David sont inscrits sur des cartons
de même format et placés dans un panier. On tire au hasard un nom du
panier. Dans chaque cas, trouvez la probabilité en pourcentage
a) de tirer Caroline
b) de ne pas tirer Caroline
c) de tirer Bernard ou David
d) de ne pas tirer Éric ni Caroline
359. Dans une boîte, Tommy place les lettres du
mot PROBABILITÉ. Trouvez la probabilité de tirer
a) un B
b) une voyelle
c) une consonne
d) un A ou un I
360. Alexia a placé dans un sac 3 jetons jaunes
marqués 1, 2 et 3. Il place dans un autre sac 3 jetons rouges marqués 4, 5
et 6. Il sort en même temps un jeton jaune et un jeton rouge et il fait la
somme des numéros. Trouvez la probabilité d'avoir une somme égale à
a) 4
b) 7
c) 9
d) 10
361. Un tableau circulaire est partagé en quatre
parties, Les mesures des angles au centre des secteurs sont respectivement
60°
pour A, 120°
pour B, 45°
pour C et 135°
pour D. Olivia lance un dard sur le tableau.
Quelle est la probabilité d’atteindre
a) la partie A
b) la partie B
c) la partie C
d) la partie D
362. Les 8 prénoms suivants : Bernard,
Caroline, David, Éric, Bernard, Julie, Caroline, David sont inscrits sur
des cartons de même format et placés dans un panier. On tire un prénom au
hasard et on ne le replace pas dans le panier.
a) Au 1er coup, le prénom David est tiré.
Quelle est la probabilité de tirer Bernard au 2e coup ?
b) Au 2e coup, le prénom David est
encore tiré. Quelle est la probabilité de tirer David au 3e
coup ?
c) Au 3e coup, le prénom Bernard est
tiré. Quelle est la probabilité de tirer Caroline au 4e coup ?
d) Au 4e coup, le prénom Julie est tiré.
Quelle est la probabilité de tirer le nom d'un garçon ?
363. Johanne prend les 28 dominos. Dans chacun des
cas, trouvez la probabilité de tirer un domino
a) dont le total des points est 8.
b) dont les points sont identiques sur les deux
demi-faces.
c) dont le total de points est plus grand que 9.
d) dont au moins une demi-face ne porte pas de
points.
364. Dans un coffre à bijoux, Cynthia a déposé 3
bracelets que nous appellerons B1, B2 et B3. Dans un autre coffre, on trouve
2 colliers : C1 et C2. Cynthia doit tirer au hasard un bracelet et un
collier de chacun des coffres.
Quelle est la probabilité d'obtenir le bracelet B2
et le collier C2 ?
365. Rosalie lance en même temps un dé et une pièce
de monnaie.
Quelle est la probabilité d'obtenir un 3 et une
face ?
366. Myriam compose des nombres de trois chiffres
différents avec 1, 2 et 3. Elle écrit ces nombres sur des jetons qu’elle
place dans un sac.
Quelle est la probabilité en pourcentage de tirer
un jeton portant un nombre supérieur à 300 ?
367. Quatre élèves, Sylvain, Jean-Luc, Anne et
Brenda se présentent à la présidence de leur école. Deux autres élèves
: François et Guillaume désirent la vice-présidence.
Combien y a-t-il de choix possibles ?
368. François lance un jeton marqué A sur un côté
et B sur l'autre. Au même moment, il lance un cube ayant sur ses faces C,
D, E, F, G et H.
Quelle est la probabilité d'obtenir B et D ?
369. Rosalie lance en même temps deux pièces de
monnaie, une de 5 ¢ et une de 10 ¢.
Quelle est la probabilité en pourcentage d'obtenir
2 faces ?
370. Dans le réseau routier ci-après, Rolande
veut partir de A et se rendre jusqu'à E en se dirigeant toujours vers la
droite. Elle choisit au hasard un chemin.
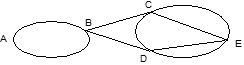
Quelle est la probabilité que ce soit ABDE ?
371. Caroline a placé dans un sac 4 boules bleues
marquées 1, 2, 3 et 4. Elle place dans un autre sac 4 boules vertes marquées
2, 3, 4 et 5. Elle sort en même temps une boule bleue et une verte. Puis,
elle fait la somme des numéros. Trouvez la probabilité d'avoir une somme
égale à
a) 5
b) 6
c) 8
d) 10
372. Richard a placé dans une boîte 5 jetons
blancs, 4 jetons verts et 7 jetons rouges. Il tire un jeton. Trouvez la
probabilité de tirer
a) un blanc
b) un vert et un rouge
c) un blanc ou un vert
d) un blanc, un vert ou un rouge
373. Ghislaine place dans un sac 4 jetons marqués
P, Q, R et S, Dans un autre sac, elle met 3 jetons marqués 7, 8 et 9.
Martin doit tirer au hasard un jeton dans chaque sac.
Quelle est la probabilité d'obtenir les jetons Q
et 7 ?
374. Toutes les lettres du mot MOTOCYCLETTE sont
placées en double dans une boîte. Quelle est la probabilité de tirer
a) un O
b) un E
c) une voyelle
d) une consonne
375. Julie place dans un sac trois cubes : un bleu,
un rouge et un jaune. Dans un autre sac, elle met deux boules : une noire et
une blanche.
Construisez un arbre qui illustre cette situation.
Chapitre
16. Statistiques Solutions
376. Vrai ou faux.
a) Un diagramme circulaire est représenté par un
rectangle.
b) La moyenne est la donnée du milieu dans un
ensemble.
c) Le mode est la donnée qui apparaît le plus
souvent dans un ensemble.
d) Un diagramme à ligne brisée s’inscrit dans
un cercle.
377. Dans un test, quatre élèves ont 80 sur 100
et trois élèves ont 60 sur 100. Trouvez
a) le mode
b) la médiane
c) la moyenne
378. Quinze élèves ont participé à une course.
Voici, en minutes, le temps enregistré par chacun : 9, 10, 12, 12, 12,
14, 15, 16, 16, 17, 17, 19, 20, 20, 21. Trouvez
a) le mode
b) la médiane
c) la moyenne
379. Dans un examen, l’enseignante décide
d’augmenter de 3 points la note de chaque élève. Qu’arrive-t-il
a) à la moyenne
b) à la médiane
c) au mode
380. La direction d'une école polyvalente décide
de faire certains classements. Dans chacun des cas, indiquez si l'étude a
un caractère quantitatif ou qualitatif.
a) Selon l'âge des élèves
b) Selon le degré d'autonomie des élèves
c) Selon le temps consacré aux devoirs
d) Selon l'habillement des élèves
381. Indiquez, pour chacune des situations
suivantes, si la variable est discrète ou continue.
a) La grandeur des élèves
b) Le nombre d'élèves par classe dans une école
c) Les gagnants d'un concours de chant
d) Le temps lors d'une course automobile
382. Voici le moyen de transport utilisé par les
200 élèves de l'école Buies : 80 élèves viennent à pied à l'école ;
36 élèves y viennent à bicyclette ; 64 y viennent en autobus ; les autres
y viennent en automobile. Trouvez la fréquence relative pour chaque moyen
de transport.
a) À pied
b) À bicyclette
c) En autobus
d) En automobile
383. En utilisant les données du problème précédent,
calculez la mesure de l'angle au centre si on utilise un diagramme
circulaire.
a) À pied
b) À bicyclette
c) En autobus
d) En automobile
384. Le revenu de Marie-Josée a été le suivant
pour chaque année donnée : 8 400 $ en 1986, 14 600 $ en 1987, 20 400 $ en
1988, 22 300 $ en 1989, 15 500 $ en 1990, 9 800 $ en 1991 et 18 900 $ en
1992.
Construisez un tableau à partir de ces données en
indiquant un titre.
385. En utilisant les données du problème précédent,
construisez un diagramme à ligne brisée.
386. Des personnes ont été interrogées afin de déterminer
leur jeu préféré. 22 personnes préfèrent les échecs, 35 personnes les
dames, 68 personnes les cartes, 15 personnes le scrabble et 52 personnes le
monopoly.
a) Quel jeu a la plus basse fréquence ?
b) Quel jeu a la plus haute fréquence ?
c) Quel est le pourcentage des personnes qui préfèrent
les échecs ?
387. En utilisant les données du problème précédent,
construisez un diagramme à bandes verticales en ordre croissant.
388. Pour chaque 10 dollars que Marc dépense, il
consacre 3 dollars à ses loisirs, 2 dollars aux vêtements, 1 dollar en
consommation et 4 dollars à l'achat de livres.
Construisez un diagramme circulaire.
389. Suzie note le titre de tous les livres qu'elle
a lus. Voici le tableau qui indique le nombre de livres lus de 2008 à 2012
:
|
Années
|
Nombre de livres lus
|
|
2008
|
32
|
|
2009
|
23
|
|
2010
|
45
|
|
2011
|
12
|
|
2012
|
33
|
Combien Suzie a-t-elle lu de livres en moyenne par
année pendant cette période ?
390. La moyenne d’un examen donné à 25 élèves
est de 70. Deux élèves de plus passent l’examen. Ils ont 50 et 80.
Quelle est la nouvelle moyenne ?
391. Le père et la mère ont 45 et 48 ans. Les
trois enfants ont 12, 10 et 7 ans.
Quelle sera la moyenne d’âge dans 10 ans ?
392. Ce diagramme indique le nombre de paires de
jeans vendues dans une boutique au cours de six mois.
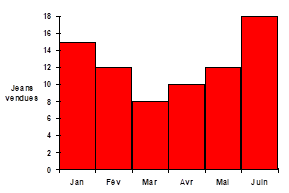
a) Quelle classe possède la plus basse fréquence
?
b) Quel type de graphique a-t-on utilisé ?
c) Déterminez la moyenne de cette distribution.
d) Déterminez le mode de cette distribution.
393. Ce tableau indique le nombre de paires de
lunettes vendues dans une lunetterie par groupe d'âge de 10 à 49 ans.
|
Groupe d'âge
|
Fréquence
|
|
10-14 ans
|
5
|
|
15-19 ans
|
18
|
|
20-24 ans
|
19
|
|
25-29 ans
|
21
|
|
30-34 ans
|
24
|
|
35-39 ans
|
18
|
|
40-44 ans
|
23
|
|
45-49 ans
|
27
|
a) À quelle classe la médiane appartient-elle ?
b) Combien de paires de lunettes ont été vendues
aux personnes ayant plus de 34 ans ?
c) Combien de paires de lunettes ont été vendues
aux personnes ayant moins de 40 ans ?
d) Quelle est la limite inférieure de la troisième
classe ?
394. La compagnie XYZ a 28 boutiques. Voici le
nombre de blouses vendues dans chaque boutique au cours du mois de juin :
43
18
37
42
63
41
77
66
35
82
49
79
68
37
49
81
45
20
35
45
65
67
60
39
30
15
40
44
Complétez le tableau de distribution ci-dessous.
|
Classe
|
Fréquence
|
Fréquence relative en %
|
|
0-19
|
|
|
|
20-39
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
395. Dans un club de vidéos, 68 personnes ont loué
des films d'action, 102 personnes des films d'aventure, 35 personnes des
films d'horreur, 42 personnes des films comiques et 16 personnes des films
fantastiques.
a) Quelle sorte de films a la plus basse fréquence
?
b) Quelle sorte de films a la plus haute fréquence
?
c) Quel est le pourcentage des personnes qui préfèrent
les films comiques ?
396. En utilisant les données du problème précédent,
construisez un tableau en plaçant les films par ordre décroissant de fréquence.
397. Le propriétaire d'un restaurant a fait des
enquêtes concernant la livraison à domicile pour son commerce. Dans chacun
des cas, indiquez si l'étude a un caractère quantitatif ou qualitatif.
a) Le nombre de personnes qui ont téléphoné par
jour
b) L'accueil des clients
c) L'état des revenus mensuellement
d) La courtoisie des livreurs
398. L’inspecteur municipal a indiqué le nombre
de personnes vivant au village par groupes d'âge.
|
Groupe d'âge
|
Fréquence
|
Fréquence cumulée croissante
|
|
0-15 ans
|
12
|
|
|
16-30 ans
|
17
|
|
|
31-45 ans
|
31
|
|
|
46-60 ans
|
23
|
|
|
61-75 ans
|
15
|
|
|
76-90 ans
|
8
|
|
|
91 ans et plus
|
1
|
|
Complétez la colonne de fréquence cumulée
croissante.
399. L'épicerie
Des Saules a vendu au cours d'une journée 28 boîtes d'avoine, 52 boîtes
de blé entier, 48 boîtes de maïs et 72 boîtes de blé soufflé.
|
Sortes de céréales
|
Fréquence
|
Fréquence relative
|
Degrés
|
|
Avoine
|
28
|
14
%
|
50,4
|
|
Blé
entier
|
|
|
|
|
Maïs
|
|
|
|
|
Blé
soufflé
|
|
|
|
Complétez le tableau en indiquant la fréquence,
la fréquence relative et les degrés de l’angle au centre dans un
diagramme circulaire.
400. Dans un groupe de 300 personnes, 102 préfèrent
le hockey, 35 le football, 28 les quilles, 68 le baseball et les autres la
course automobile.
Construisez un diagramme à bandes verticales.
----
FIN ----
![]()
![]()