Récréations géométriques

Série A

16. Julius sourit

Julius dessine une grille 6 × 6. Il partage la grille en huit parties de même forme et de même grandeur. Quatre cases ne font pas partie du partage. Ce sont les cases dans lesquelles Julius a dessiné son visage.

				K

	K
				K

	K

Quand il a terminé, il dit à Martin :
- Tu dois partager la grille en huit parties de même forme et de même grandeur. Aucune partie ne contient un visage.

Faites le partage.

Solution

Combien de régions distinctes au minimum peut-on obtenir en traçant trois droites ?

Solution

Série B

16. Devoir de Gisèle

Gisèle dessine la grille ci-dessous qui est composée de carrés unitaires. Elle dit à ses élèves :

- Vous voyez bien qu’il y a 22 carrés dans cette figure. Mais si vous regardez attentivement, vous pourrez en compter d’autres.

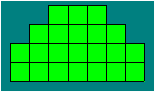
Combien peut-on compter de carrés de toute grandeur dans cette figure, autres que les carrés unitaires ?

Solution

Il y a deux sortes d’esprit : l’esprit de géométrie et l’esprit de finesse.

Blaise Pascal (1623-1662)

Série C

16. Un rectangle 5 ´ 6

Prenez huit pièces, dont quatre L et au plus deux de chaque autre modèle.

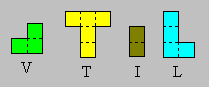
Construisez un rectangle 5 ´ 6.

Solution

Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles entre elles.