Série A

Solution 25

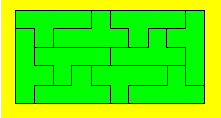
Comme un pentomino est formé de cinq carrés et qu’il y a 10 pièces, le rectangle doit avoir une aire de 50 unités carrées. Deux rectangles sont théoriquement possibles : le 1 × 50 et le 2 × 25. Comme le 1 × 50 est impossible, il reste le 2 × 25. Les bordures de cinq unités doivent être chacune formées par un pentomino placé en hauteur. Pour compléter chacune de ces bordures, on place un pentomino en longueur et on continue. Voici une configuration possible :

Retour au problème

Série B

Solution 25

William a délimité un rectangle 7 × 11 : ce qui fait 77 sous. Son père a utilisé six sous. Les deux sous au-dessus du rectangle ne peuvent pas être utilisés. Il reste 69 sous. Si on les partage en groupes de six, cela donne 11 groupes et un demi. Il y aurait donc théoriquement une possibilité de 11 rectangles 2 × 3. Voici une façon de partager la figure pour obtenir 11 rectangles :

Retour au problème

Série C

Solution 25

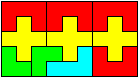
Voici une façon de disposer les pièces :

Retour au problème

Selon l’astronome Galilée (1564-1642), les mathématiques servent principalement à peser les ignorants, à mesurer les sots et à compter les uns et les autres.