Série A

Solution 100

On complète la colonne du 8 de pique et du 7 carreau par un 4 (indice 4). C’est le 4 de cœur, car une carte de carreau est déjà posée (indice 1). Ces cartes sont dans la première colonne (indice 3). Dans le coin supérieur droit, il y a une carte de carreau et dans le coin inférieur droit une carte de cœur (indice 6). Dans cette dernière case, on place le 2 de cœur, car c’est la seule carte de cœur qui reste. On place le 4 de carreau au centre (indices 1 et 5). Le 5 de trèfle est au milieu de la première ligne (indice 5). On complète la première ligne par le 10 de cœur, la deuxième ligne par le 7 de trèfle et la deuxième colonne par le 10 de pique (indice 2). Voici le tableau qui illustre la position des cartes :

Retour au problème

Le tac-tix est un jeu qui est une variante du nim et qui a été imaginé par le mathématicien danois Piet Hein.

Série B

Solution 100

Les combinaisons possibles de trois nombres pairs (2 à 14) dont la somme est 24 sont : (2, 8, 14), (2, 10, 12), (4, 6, 14), (4, 8, 12), (6, 8, 10). Il y a trois rangées de trois enclos qui passent par M. Seul 8 apparaît trois fois dans les combinaisons. 

Il doit y avoir huit lapins dans l’enclos M.

Retour au problème

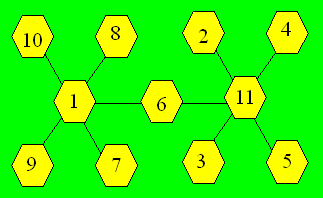
La somme des nombres de 1 à 11 est 66. Comme il y a cinq rangées, on fait : 5 ´ 18 = 90, 90 - 66 = 24 et 24 ¸ 2 = 12. La somme des nombres des deux cellules qui appartiennent à trois rangées est 12. Les combinaisons possibles sont : (1, 11), (2, 10), (3, 9), (4, 8), (5, 7). Une configuration est :