Série A

Solution 13

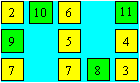
Les cases vertes contiennent 8, 9 et 10. La case verte de la première colonne ne peut recevoir 10, car il n’y a pas de 1. La seule combinaison de trois nombres qui peut être placé dans la deuxième colonne est (5, 6, 7). Deux combinaisons comportent un 7 : (2, 7, 9) et (3, 7, 8). Deux combinaisons comportent un 11 : (2, 5, 11) et (3, 4, 11). À cause du 5 qui est dans la deuxième colonne, on retient la combinaison (3, 4, 11). Comme le 3 est dans la troisième colonne, il ne peut être dans la première. C’est donc la combinaison (2, 7, 9) qui est dans la première colonne. On obtient la disposition suivante.

Série B

Solution 13

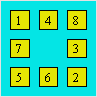
Les combinaisons de trois nombres dont la somme est 13 sont (1, 4, 8), (1, 5, 7), (2, 3, 8), (2, 4, 7), (2, 5, 6) et (3, 4, 6). Le 8 apparaît deux fois dans les combinaisons. On le place dans un coin et on complète les deux rangées qui touchent à 8 avec (1, 4) pour l’une et avec (2, 3) pour l’autre. On connaît la position du 1. On complète les rangées en se servant des combinaisons. Voici une configuration :

Série C

Solution 13

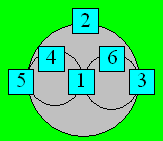
Les combinaisons de trois nombres dont la somme est 10 sont : (1, 3, 6), (1, 4, 5), (2, 3, 5). Le 1 appartient à deux combinaisons, tout comme le 3 et le 5. Les trois nombres sont placés dans la rangée horizontale inférieure. Une configuration est :