Série A

Solution 21

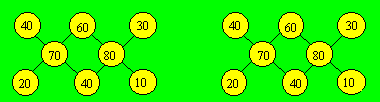
Les combinaisons de trois nombres dont la somme est 150 sont : (10, 60, 80), (20, 60, 70), (30, 40, 80) et (40, 40, 70). Le 10, le 20 et le 30 n’apparaissent chacun qu’une seule fois dans les combinaisons. On doit donc les placer dans des coins. Après avoir placé le 10, on doit donc prendre la combinaison (10, 60, 80). Si on place 60 au centre, on doit placer obliquement (20, 60, 70). Comme 20 n’apparaît qu’une seule fois, on doit le placer dans un coin. On complète. On obtient la disposition de gauche. Après avoir placé le 10, puis le 80 au centre, on obtient la disposition de droite.

Retour au problème

Série B

Solution 21

On doit partager 56 prunes : 28 dans les six paniers de gauche et 28 dans les trois paniers de droite. Les paniers de droite reçoivent 7, 10 et 11 prunes. Les combinaisons pour 7 sont (2, 5) et (3, 4) ; celles pour 10 sont (2, 8) et (4, 6) ; celles pour 11 sont (3, 8) et (5, 6). Il y a deux façons de partager les prunes. Les voici :

Retour au problème

Série C

Solution 21

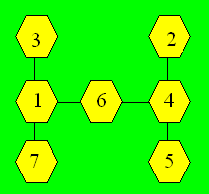
Les combinaisons de trois nombres dont la somme est 11 sont : (1, 3, 7), (1, 4, 6), (2, 3, 6), (2, 4, 5). Le 5 et le 7 ne sont qu’une seule fois dans les combinaisons. Ils ne peuvent pas apparaître dans les cellules extrêmes de la rangée horizontale. Une combinaison est :

Retour au problème