|
Série A
Solution 44
Il faut partager 20 + 94
= 114 en six rangées. Il y aura 114 ¸ 6 = 19 billes
par rangée. Trois combinaisons de six nombres sont possibles : un 4 et cinq
3 ; deux 4 trois 3 et un 2 ; trois 4, un trois et deux 2. Il y a une seule combinaison pour les rangées où il n’y a
pas de 2. Elle contient quatre 3 et un 4. On peut compléter la
cinquième rangée verticale, la sixième rangée verticale, la cinquième rangée
horizontale avec des 3 ; la
deuxième rangée verticale avec des 4 ; la
deuxième,
la troisième rangée horizontale, la première diagonale avec des 3 ; la
première rangée horizontale avec des 4 et ainsi de suite. La grille remplie est :
|
3 |
2 |
4 |
4 |
3 |
3 |
|
3 |
4 |
3 |
3 |
3 |
3 |
|
2 |
4 |
3 |
3 |
4 |
3 |
|
4 |
2 |
3 |
3 |
3 |
4 |
|
3 |
3 |
4 |
3 |
3 |
3 |
|
4 |
4 |
2 |
3 |
3 |
3 |
Retour
au problème
|
Le
premier recueil imprimé de récréations mathématiques fut publié en
1612 sous le titre de Problèmes plaisans et délectables qui se font
par les nombres.
|
|
Série B
Solution 44
La somme de tous les numéros est 54 ; celle des numéros d’une rangée
horizontale (ou verticale) est 54/3 = 18. Le nombre du milieu est 18/3 = 6. On
intervertit le 3 et le 6. On vérifie la somme des nombres de chaque rangée. On
intervertit le 1 et le 5. Voici la nouvelle figure :

Retour
au problème
|
L'économie
est une science qui est seulement à la portée des riches.
Henri Murger
|
|
Série C
Solution 44
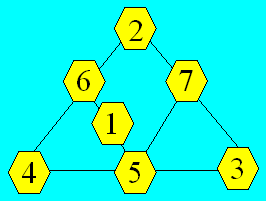
Il existe une seule combinaison de deux nombres dont la somme
est 12 : (5, 7). Deux triplets contiennent un 5 : (1, 5, 6) et (3, 4,
5). Deux triplets contiennent un 7 : (1, 4, 7) et (2, 3, 7). Une
configuration est :
Retour
au problème
|
Solution
de l’énigme
Un parallélogramme
|
![]()
![]()