|
| |
|

|
Récréations
magiques |
|
Série A
Solution 75
On cherche les combinaisons possibles de quatre entiers de 1
à 9 dont la somme est 20 et la somme de leurs carrés. Voici les
résultats :
|
Combinaisons |
Somme des carrés |
|
(1, 2, 8, 9) |
150 |
|
(1, 3, 7, 9) |
140 |
|
(1, 4, 6, 9) |
134 |
|
(1, 4, 7, 8) |
130 |
|
(1, 5, 6, 8) |
126 |
|
(2, 3, 6, 9) |
130 |
|
(2, 3, 7, 8) |
126 |
|
(2, 4, 5, 9) |
126 |
|
(2, 4, 6, 8) |
120 |
|
(2, 5, 6, 7) |
114 |
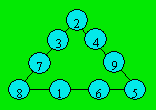
On voit qu’il y a trois combinaisons dont la somme des
carrés est 126. Dans ces trois combinaisons, le 2, le 5 et le 8 apparaissent
une seule fois. On les place aux sommets. On obtient cette disposition.
Retour
au problème
|
Un
octogramme est un polygone étoilé
régulier à huit branches ou pointes.
|
|
Série B
Solution 75
Il y a trois groupes de deux pièces
qui totalisent 22 florins : (7, 15), (9, 13) et (10, 12). Le dernier groupe
formé de pairs doit être placé à gauche, le 12 étant à gauche. On
complète la première colonne avec 7 et 5 dans l’ordre. On écrit 15 dans le
cercle du milieu en base. En complétant, on obtient cette configuration.

Retour
au problème
|
L’ordre
d’une chaîne numérique est
le nombre de termes ou de maillons.
|
|
Série C
Solution 75
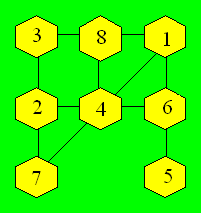
Il existe deux
combinaisons possibles pour la rangée de deux cellules : (4, 8) et
(5, 7). Les combinaisons de trois nombres dont la somme est 12 sont :
(1, 3, 8), (1, 4, 7), (1, 5, 6), (2, 3, 7), (2, 4, 6) et (3, 4, 5). Une
configuration est :
Retour
au problème
|
Solution
de l’énigme
Le nombre est 11,5. |
| |
|
|
![]()
![]()