|
Série A
57. Âge de Starbek
Starbek est un animal intelligent qui vit sur une planète
perdue dans la galaxie. Comme les autres habitants, Starbek se sert des quatre
cristaux qui ornent son front. Il compte ainsi :
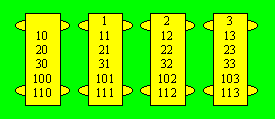
À l’entrée de sa taverne (!), Starbek écrit son âge.
Actuellement, on peut lire 333 ans.
Quel est l’âge de Starbek dans notre
système ?
Solution
|
Ce
qui est plus fort que l'éléphant, c'est la brousse.
Proverbe africain
|
|
Série B
57.
Au Vieux Quai
Près
du Vieux Quai, trois kiosques ont été installés. Sur chacun, on a inscrit un
numéro comme ci-dessous. Chaque numéro élevé au cube correspond au nombre de
figurines qui se trouvent à l’intérieur. Dans cet exemple, il y a 27
figurines dans le premier kiosque, 343 dans le deuxième et 1 dans le
troisième, soit un total de 371.

Après la vente de toutes les figurines, un
nouveau stock a été réparti en respectant la même règle. On a alors donné
le numéro 5 à un kiosque. De plus, on peut lire un nombre inférieur à 200.
Combien y a-t-il de figurines dans les trois kiosques ?
Solution
|
Quel
est le 4e plus petit nombre, en excluant zéro, qui est
divisible à la fois par 4 et par 6 ?
Solution
|
|
Série C
57.
Multiples d’un parfait
Régis a dessiné la
grille ci-après et a noirci cinq cases. Il sait que 28 est un nombre parfait.
Aussi, il décide de placer dans la grille seulement des multiples de 28, sauf
pour les nombres d’un seul chiffre qui n’obéissent à aucune règle. Les
nombres sont lus horizontalement et verticalement. Cinq chiffres sont en bonne
position.
Remplissez la grille en plaçant un chiffre par case.
Solution
© Charles-É.
Jean
|
Au
bout de six ans, le calendrier d’une année ordinaire est le même si
on a une seule année bissextile dans l’intervalle, y inclus la
dernière année.
|
![]()
![]()