|
Série A
Solution 17
Le nombre de pains aux
bleuets appartient à la suite : 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67,
73, 79, 85, 91 et 97. Les nombres ayant un 3 sont 13, 31, 43 et 73. On fait 100
- 13 = 87 ; 100 - 31 = 69, 100 - 43 = 57 et 100 - 73 = 27. Seuls 69 et 57
peuvent être divisés par 4 avec un reste de 1. On rejette 69 car il a un 9.
Alcibia
a pétri 57 pains aux fraises et 43 pains aux bleuets.
Retour
au problème
|
Un
ensemble de
Cantor
est un ensemble infini de points qui demeurent à la
suite du partage d'un segment en tiers fait d'une façon indéfinie.
|
|
Série
B
Solution 17
Le premier chiffre
peut être 3 (indice 4). Alors, le deuxième chiffre est 6 (indice 1) ; le
troisième chiffre est 1 (indice 2) ; le quatrième chiffre est 7
(indice 3) ; le dernier chiffre est 0. La somme est 17. Le premier chiffre
peut être 4 (indice 4). Alors, le deuxième chiffre est 7 (indice 1) ; le
troisième chiffre est 2 (indice 2) ; le quatrième chiffre est 9
(indice 3) ; le dernier chiffre est 1. La somme est 23. Le premier chiffre
ne peut pas être supérieur à 4.
Le numéro est 47291.
Retour
au problème
|
Solution de l'énigme
La différence de deux nombres impairs consécutifs est toujours 2.
|
|
Série
C
Solution 17
On
donne aux quatre briques inférieures les valeurs a, b, c
et d comme il est montré ci-après. On complète chacune des briques non
marquées. On peut écrire : c + d = 9. On peut
écrire : a + b + 8 = 18. D’où, a + b = 10.
On peut écrire : 3b + 2c + 13 = 25. D’où, 3b + 2c
= 12. De cette dernière équation, on trouve b = 2 et c = 3.
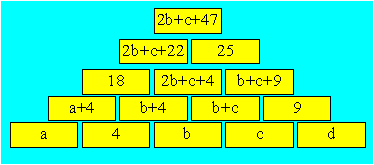
Le nombre qui devrait apparaître dans la brique supérieure
est 54.
Retour
au problème
|
On retrouve chez certains animaux des facettes de l’intelligence
humaine, comme la perception, la mémoire, l’attention, l’imagination,
le jugement et le raisonnement.
|
![]()
![]()