|
| |
|

|
Récréations
numériques |
|
Série A
Solution 69
Dans le coin inférieur gauche, on trouve cinq et huit
crayons. Pour arriver à 8, il est nécessaire d’avoir 12 crayons dans
les deux canettes de la rangée inférieure. La deuxième canette de cette
rangée a sept crayons. La canette du milieu de la figure a au moins quatre
crayons, car il y a au moins un crayon dans chaque canette. Si cette canette a
quatre crayons, la troisième de la rangée inférieure a un crayon : ce
qui est impossible car la troisième canette de la deuxième rangée aurait -1
crayon. Si cette canette a cinq crayons, la troisième de la rangée inférieure
a deux crayons : ce qui est impossible car la troisième canette de la
deuxième rangée n’aurait aucun crayon. Si cette canette a six crayons, la
troisième de la rangée inférieure a trois crayons. La troisième canette de
la deuxième rangée a un crayon. Les crayons sont disposés ainsi :
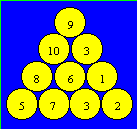
Tania a 54 boîtes de crayons en tout.
Retour
au problème
|
Un
carré magique
gnomonique est un arrangement carré d'ordre n dans lequel la somme
des nombres de chacun des quatre gnomons est identique.
|
|
Série
B
Solution 69
De 1 à 99, on a les 10 chiffres 2 des
dizaines et les 10 chiffres des unités : ce qui fait 20 chiffres 2. De 100
à 199, on a aussi 20 chiffres 2. De 200 à 299, on a les 100 chiffres 2 des
centaines et les 20 chiffres des dizaines et des unités : ce qui fait en
tout 160 chiffres 2. Il reste deux chiffres 2 à inscrire. On écrit 302 et
312.
La collection d’Alice
contient 312 soldats de plomb.
Retour
au problème
|
L’Anthologie grecque
contient de nombreuses récréations dont neuf de temps.
|
|
Série
C
Solution 69
On
construit un tableau dans lequel on suppose pour le premier entier une valeur de
1 à 7. On calcule la somme et la racine carrée de la somme.
|
Premier entier a |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Somme |
9 |
49 |
169 |
441 |
961 |
1849 |
3249 |
|
Racine carrée |
3 |
7 |
13 |
21 |
31 |
43 |
57 |
|
Racine carrée – 1 |
2 |
6 |
12 |
20 |
30 |
42 |
56 |
Les résultats de la dernière ligne sont le produit de deux
entiers consécutifs : 1 ´ 2 = 2, 2 ´
3 = 6, 3 ´ 4 = 12, etc.
Pour trouver le résultat
des opérations indiquées sans extraire la racine carrée, on multiplie le
nombre choisi par l'entier qui le suit et on additionne 1 à ce produit. Si le
premier nombre choisi est 5, le résultat final est : 5 × 6 + 1 =
31. Ce résultat est la racine carrée de 961.
Retour
au problème
|
Solution
de l’énigme
Cinq
enfants
|
| |
|
|
![]()
![]()