Nombre d’éléments dans un ensemble. Selon le nombre d’éléments, certains ensembles ont reçu une appellation.

Ensemble vide
Ensemble qui n'a pas d'élément. On écrit alors { } ou Ø. Le cardinal de l'ensemble est 0.

Singleton
Ensemble qui a un seul élément. Exemple : {12}. L’élément unique est 12. Le cardinal de l'ensemble est 1.

Paire
Ensemble qui a deux éléments. Exemple : {mardi, 19}. Les deux éléments sont mardi et 19. Le cardinal de l'ensemble est 2.

Ensemble fini
Ensemble qui a un nombre fini d'éléments. Dans la pratique, il s'avère parfois difficile de tous les compter. Par exemple, l'ensemble des sapins d’un territoire donné est un ensemble fini. Le cardinal d'un ensemble fini correspond à un entier naturel.

Ensemble infini
Ensemble qui a un nombre infini d'éléments. Par exemple, l'ensemble des nombres pairs est un ensemble infini. Il existe toujours un nombre pair plus grand que le nombre qu'on croirait le plus grand.

Ensembles équivalents
Deux ensembles sont équivalents si à chaque élément du premier correspond un et un seul élément du second et si à chaque élément du second correspond un et un seul élément du premier. Les deux ensembles sont alors dits en correspondance biunivoque. Ils ont conséquemment le même nombre d'éléments, soit le même cardinal. 

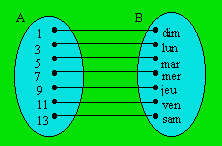
Ainsi A = {x | x est un nombre impair inférieur à 14} et B = {x | x est un jour de la semaine} sont des ensembles équivalents. On peut représenter cette situation ainsi :

On pourrait aussi représenter graphiquement cette situation. On dessine alors deux diagrammes de Venn et on associe deux à deux les éléments.

Ensembles égaux
Deux ensembles sont égaux quand ils ont les mêmes éléments. Il va de soi qu'ils ont aussi le même nombre d'éléments. Soit C = {6, 3, 4} et D = {6/2, 12/3, 24/4}, alors C = D. Par exemple, si E = Ø et F = {0}, E n'est pas égal à F.

Ensembles disjoints
Deux ensembles sont disjoints quand ils n’ont aucun élément commun. Par exemple A = {a, b, c} et B = {1, 7, 9, 11} sont disjoints.