Nœud d’un réseau

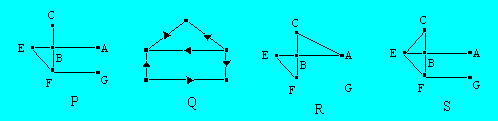
Point d’intersection des lignes. Dans le réseau P, les sommets A, B, C, E, F et G sont des nœuds du réseau.

Branche d’un réseau

Toute ligne qui forme le réseau et qui est limitée par des nœuds. Les branches qui touchent à B sont BA, BC, BE et BF dans le réseau P.

Degré d’un nœud

Nombre de branches qui aboutissent en un nœud. Le degré du nœud B est 4 dans le réseau P.

Nœud terminal

Nœud qui termine une ligne. Il est de degré 1. A, C et G sont des nœuds terminaux dans le réseau P.

Nœud de relais

Point de rencontres de deux branches. Il est de degré 2. Le seul nœud de relais est E dans le réseau P.

Nœud carrefour

Point de rencontre de trois branches ou plus. Il est de degré 3 ou supérieur à 3. B et F sont des nœuds carrefours dans le réseau P.

Chemin

Séquence de branches qui sont parcourues. De A à G, le chemin est AB, BE, EF et FG dans le réseau P.

Réseau simple

Un réseau est simple si chaque nœud est de degré inférieur à 3. Le réseau P n’est pas simple, car le degré de B est 4.

Réseau fermé

Un réseau est fermé s’il n’a pas de nœud terminal. Le réseau P n’est pas fermé. Il a au moins un nœud terminal : A, C et G.

Réseau connexe

Un réseau est connexe si on peut le parcourir en entier. Le réseau P est connexe. De A à C, on peut suivre le chemin : AB, BE, EF, FG, GF, FB et FC. On a dû passer deux fois sur FG.

Réseau orienté

Un réseau est orienté lorsqu’il est muni d’un sens. Le réseau Q est orienté.

Réseau unicursal ou eulérien

Un réseau est unicursal ou eulérien s’il peut être parcouru en passant une fois et une seule fois par chaque branche. On peut parcourir en entier le réseau R ainsi : AB, BE, EF, FB, BC et CA.

Réseau hamiltonien

Un réseau est hamiltonien s’il peut être parcouru en passant une fois et une seule fois par chaque nœud. Dans le réseau S, on peut passer par tous les nœuds une seule fois ainsi : AB, BC, CE, EF et FG.

On peut passer par toutes les branches d’un réseau une et une seule fois aux conditions suivantes :

1^e Tous les nœuds sont de degré pair. On peut alors partir de n’importe lequel point et finir à ce point choisi.

2^e Deux nœuds sont impairs et les autres pairs. On part d’un de ces points et on termine à l’autre.

3^e Plus de deux nœuds sont impairs. Il est impossible de parcourir le réseau en passant une seule fois par les branches.

Voici quelques propriétés des réseaux :

1. La somme des degrés des nœuds est toujours paire.

2. La somme des degrés des nœuds est toujours égale au double du nombre de branches.

3. Dans un réseau, il y a toujours un nombre pair de nœuds à degré impair.

4. La somme du nombre de nœuds et du nombre de régions est égale au nombre de branches augmenté de 2.