1^e Figure formée par des points, appelés nœuds, disposés d'une manière quelconque et reliés entre eux par des lignes appelées branches. Les principales récréations consistent à déterminer le chemin le plus court d'un point donné à un autre ; à établir si le réseau peut être parcouru en entier et de quelle façon ; à déterminer le nombre de chemins distincts qui couvrent entièrement un réseau. 

En mathématiques récréatives, la terminologie des réseaux est souvent confondue avec celle des graphes. Plusieurs jeux, comme la marelle, se jouent sur un réseau. Voici un réseau :

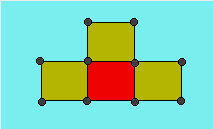
Quatre règles peuvent être appliquées à des réseaux :

1. La somme des degrés des nœuds est égale au double du nombre de branches.

2. La somme du nombre de nœuds et du nombre de régions intérieures est égale au nombre de branches augmenté de l'unité.

3. La somme des degrés des nœuds est toujours paire.

4. Le nombre de nœuds de degré impair est toujours pair.

Pour chacun des trois réseaux ci-dessous, le degré de chaque sommet est indiqué.

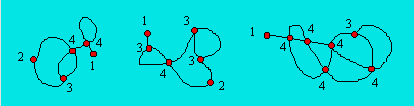
On peut vérifier ces règles dans les réseaux ci-dessus en consultant ce tableau.

Un réseau peut être bicursal, hamiltonien, multicursal, unicursal ou valué.

2^e Jeu imaginé par T. P. Truran en 1975 et dont le tablier est une feuille de papier. Au départ, les joueurs dessinent alternativement une branche jusqu'à ce que le réseau dessiné soit accepté de part et d'autre. Par la suite, le premier joueur part d'un sommet choisi et parcourt une branche. Le second joueur part du sommet laissé par son adversaire et parcourt également une branche. Cette séquence se poursuit jusqu'à ce qu'un joueur ne puisse plus avancer, car il n'y a plus de branche libre. Ce dernier joueur est le perdant. 

Ce jeu appartient à la classe des jeux de papier et de crayon.

© Charles-É. Jean

Index : R

Voir aussi Réseau dans l'Aide-mémoire.

Voir Récréation topologique