|
| |
|
|
Défis |
|
Série A
21. Macarons de Karo
Karo
a préparé le tableau ci-après composé de trois cases noires. Elle doit
disposer dans les cases grises 12 macarons numérotés de 1 à 12. Elle place d’abord
les macarons 10, 3 et 4 dans les positions données.
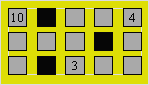
Disposez les autres
macarons de façon que leur somme soit 17 dans chaque rangée de trois macarons
voisins horizontalement et verticalement.
Solution
|
Dans un jeu Qui perd gagne, c’est le joueur perdant qui est le
gagnant. En anglais, on dit jouer "misère", en utilisant ce mot en
français.
|
|
Série B
21. École de Marjo
Marjo, une enseignante, rencontre la secrétaire de l’école. Voici un extrait de leur
conversation :
Enseignante.
- Vous voulez savoir combien j’ai d’élèves ?
Secrétaire.
- C’est exact.
Enseignante.
- Le nombre augmenté de 64 est égal à trois fois ce nombre augmenté de 6.
Secrétaire. -
Wow ! ! ! Je calcule.
Combien y a-t-il d’élèves dans cette classe ?
Solution
|
La différence de
deux carrés est égale au produit de la somme et de la différence des
deux bases. Par exemple, 182
- 132
= 31 ´
5.
|
|
Série C
21. Initiale de
Mathias
Maude a préparé
le tableau ci-après. D’une figure à l’autre, une colonne est ajoutée. Les
lettres sont écrites en ordre alphabétique à partir du coin supérieur gauche
de chaque figure. Après un Z, Maude recommence à A.
|
A |
B |
C |
|
I |
J |
K |
L |
|
S |
T |
U |
V |
W |
|
H |
|
D |
|
R |
|
|
M |
|
D |
|
|
|
X |
|
G |
F |
E |
|
Q |
P |
O |
N |
|
C |
B |
A |
Z |
Y |
Trouvez un algorithme qui permet de déterminer le rang
alphabétique de la lettre du coin inférieur droit et ce, dans une figure dont
le nombre de cases de la dernière ligne est donné.
Solution
© Charles-É. Jean
|
J’écris quatre
nombres : 27, 37, 47 et 57. Parmi eux, combien sont des nombres
premiers ?
Solution
|
|
|
|
|
![]()
![]()