|
Série A
54. Tigres de Maude
Maude
prépare une grille carrée 2 ´
2 et trace les six obliques comme ci-après. Elle décide maintenant de former
une grille 9 × 9. Quand elle a terminé de tracer sa grille, elle dessine un
tigre dans les quatre cases des coins. Il est alors interdit de passer des
obliques par ces cases.
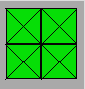
Combien Maude
pourra-t-elle tracer d’obliques au maximum ?
Solution
|
À
tous les deux ans, pour un même quantième et un même mois, le jour de
la semaine avance de deux rangs quand il n’y a pas de 29 février
dans l’intervalle.
|
|
Série B
54. Coups de mains
Dans la
classe de Céline, il y a 18 élèves. Chacun prend un numéro de 3 à 20.

Les élèves qui ont des numéros divisibles par 3 doivent
donner la main à chacun des élèves dont le numéro est un nombre premier. Les
élèves qui ont des numéros divisibles par 4 doivent donner la main à chacun
des élèves dont le numéro est un nombre pair divisible par 3.
Combien de poignées de mains seront échangées ?
Solution
|
Le
décryptage consiste à remettre dans sa forme primitive un texte
chiffré dont on ne connaît pas le code.
|
|
Série C
54. Repères de
Mathis
À
partir de 2, dans le tableau ci-après, Mathis a écrit des entiers en
augmentant de 3 d’une case à l’autre.
|
2 |
5 |
8 |
11 |
14 |
17 |
|
20 |
23 |
26 |
29 |
32 |
35 |
|
38 |
41 |
44 |
... |
... |
... |
Trouvez un algorithme qui permet de déterminer si un nombre donné devrait
apparaître dans le tableau. Si oui, l’algorithme doit permettre de
déterminer le rang de la ligne et de la colonne.
Solution
© Charles-É.
Jean
|
Comment
appelle-t-on un triangle dont un angle mesure 43 degrés et l’autre 47
degrés ?
Solution
|
![]()
![]()