|
Série A
Solution 1
Si D = 4 et E = 5, le numérateur serait 20 : ce qui ferait une somme de
29 au lieu de 41. Si D = 4 et E = 6, le numérateur serait 24 : ce qui
ferait une somme de 34. Si D = 4 et E = 7, le numérateur serait 28 : ce
qui ferait une somme de 39. Si D = 5 et E = 6, le numérateur serait 30 : ce
qui ferait une somme de 41. La seule combinaison possible est (9, 10, 11).
Une disposition
est : (9 + 10 + 11)/5 = 6. On peut intervertir le 5 et le 6.
Retour
au problème
|
Je veux bien que
les gens regardent leur montre quand je donne une conférence. Ce que je
ne supporte pas, c’est qu’ils la portent à leur oreille pour
vérifier qu’elle n’est pas arrêtée.
Marcel Achard
|
|
Série B
Solution 1
On ajoute
la septième pomme en un lieu tel que la distance entre cette pomme et chacune
des deux pommes voisines obliquement est la même que la distance entre la pomme
du bas au centre et chacune des deux pommes voisines obliquement. Une disposition est :
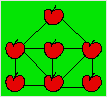
Retour
au problème
|
À 16 ans, le
mathématicien français Blaise Pascal (1623-1662) écrivit un traité
sur les coniques.
|
|
Série C
Solution 1
Il faut trouver deux carrés
dont la somme est un carré. Comme la différence des bases est 3, les trois
bases doivent former une suite arithmétique de raison 3. Le plus petit triplet
dont la somme des carrés des deux premiers est égale au carré du troisième
est (3, 4, 5). On multiplie par 3 les bases. Cela donne le triplet (9, 12, 15).
Les filles ont cueilli 81 abricots, les garçons 144 abricots.
En tout, ils ont cueilli 225 haricots.
Retour
au problème
|
Solution
de l'énigme
Au minimum, il y a trois paires de côtés communs. La nouvelle figure
aura 12 côtés.
|
![]()
![]()