Cible

Objet de récréations. La cible est formée par un ensemble de cercles ou de carrés concentriques formant des régions distinctes. Chaque région est marquée par un nombre qui correspond à des points. Certaines sous-régions peuvent valoir, par exemple, le double ou le triple des points inscrits. Les récréations consistent à déterminer, à partir du résultat final, les régions atteintes et à établir des probabilités d'atteinte de régions en fonction de leur aire.

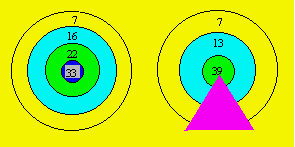
Pour réussir 100 en cinq lancers dans la première cible, le joueur devra atteindre 33 une fois, 22 deux fois, 16 une fois et 7 une fois. Dans la seconde cible, où la région grisée compte pour le double des points, pour réussir 100 en cinq lancers, le joueur devra atteindre, dans les régions non grisées, 39 une fois, 7 une fois ; puis, dans les régions grisées, 13 une fois et 7 deux fois. 

On peut imaginer d'autres cibles comme un carré magique, un carré latin, une feuille de calendrier. Voici deux autres exemples :

Dans le premier cas, les cases contiennent les 14 premiers numéros du saut du cavalier. Dans le second, les extrémités de gauche et de droite contiennent les nombres les plus élevés. 

Les problèmes de cible appartiennent à la classe des récréations numériques.

© Charles-É. Jean

Index : C