|
Composé
°
Nombre composé. – Entier naturel
qui
est le produit de deux nombres premiers ou plus. La classe des nombres composés
comprend tous les entiers naturels à l’exception de 1 et des nombres
premiers.
Le tableau suivant donne les 10 plus petits nombres composés, leurs
facteurs, leurs facteurs premiers et leur factorisation.
|
|
Facteurs |
Facteurs premiers |
Factorisation |
|
4 |
1, 2, 4 |
2 |
2 × 2 = 22 |
|
6 |
1, 2, 3, 6 |
2, 3 |
2 × 3 |
|
8 |
1, 2, 4, 8 |
2 |
2 × 2 × 2 = 23 |
|
9 |
1, 3, 9 |
3 |
3 × 3 = 32 |
|
10 |
1, 2, 5, 10 |
2, 5 |
2 × 5 |
|
12 |
1, 2, 3, 4, 6, 12 |
2, 3 |
2 × 2 × 3 = 22 × 3 |
|
14 |
1, 2, 7, 14 |
2, 7 |
2 × 7 |
|
15 |
1, 3, 5, 15 |
3, 5 |
3 × 5 |
|
16 |
1, 2, 4, 8, 16 |
2 |
2 × 2 × 2 × 2 = 24 |
|
18 |
1, 2, 3, 6, 9, 18 |
2, 3 |
2 × 3 × 3 = 2 × 32 |
Un nombre est composé lorsque l’unité du nombre d’au
moins deux chiffres est 0, 2, 4, 5, 6 ou 8. Pour établir si un nombre impair
autre que se terminant par 5 est composé, on vérifie si le nombre donné est
successivement divisible par un nombre premier inférieur à sa racine carrée.
Si on ne trouve pas de facteur premier dans l’intervalle donné, le nombre n’est
pas composé.
Par exemple, 559 est-il composé ? La racine carrée de 559
est approximativement 23,64. Les facteurs premiers possibles sont 3, 5, 7, 11,
13, 17, 19 et 23. On vérifie pour chacun de ces facteurs. On trouve que 13 est
un facteur. D’où, 559 est un nombre composé.
Henry E. Dudeney (1857-1930) a
donné l’algorithme suivant qui génère des nombres consécutifs
composés. On écrit n2 nombres
consécutifs de 2 à (n2 + 1). On
identifie les nombres premiers dans cet intervalle et on les multiplie. Au
produit, on additionne successivement les n2 entiers
trouvés. Si n est égal à 2, on écrit : 2, 3, 4 et 5. Dans cette
suite, les premiers sont 2, 3 et 5. Leur produit est 30. Les quatre nombres
composés consécutifs sont : 32, 33, 34 et 35. Si n est égal à 3,
on écrit : 2, 3, 4, 5, 6, 7, 8, 9 et 10. On fait 2 ´
3 ´ 5 ´ 7 = 210. Les
neuf nombres composés sont les entiers consécutifs de 212 à 220. Cet
algorithme donne une seule solution pour chaque valeur de n ; cette
solution n’est pas nécessairement la plus petite.
La décomposition en facteurs
d'un nombre composé peut être représentée sous forme d'un
arbre. Voici un exemple avec 420 :
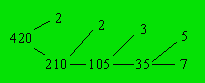
La factorisation est : 2 × 2 × 3 × 5 × 7.
Le mathématicien indien S. P. Sundaram
a créé, en 1934, un crible qui permet d’établir la liste des nombres
composés impairs. On peut présenter le crible comme une table de
multiplication de nombres impairs à partir de 3. Chaque ligne et chaque colonne
sont composées de suites arithmétiques dont la raison est donnée à droite et
en bas.
|
´ |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
... |
R |
|
3 |
9 |
15 |
21 |
27 |
33 |
39 |
45 |
51 |
... |
6 |
|
5 |
|
25 |
35 |
45 |
55 |
65 |
75 |
85 |
... |
10 |
|
7 |
|
|
49 |
63 |
77 |
91 |
105 |
119 |
... |
14 |
|
9 |
|
|
|
81 |
99 |
117 |
135 |
153 |
... |
18 |
|
11 |
|
|
|
|
121 |
143 |
165 |
187 |
... |
22 |
|
13 |
|
|
|
|
|
169 |
195 |
221 |
... |
26 |
| |
... |
... |
... |
... |
... |
... |
... |
... |
|
|
| |
|
10 |
14 |
18 |
22 |
26 |
30 |
34 |
|
|
Comme cette table contient tous les
nombres composés impairs, tout nombre impair absent du tableau est un nombre
premier. Par exemple, à partir de 9, les nombres impairs absents sont :
11, 13, 17, 19, 23, 29, 31, ... Ce sont bien des nombres premiers.
© Charles-É. Jean
Index
: C
|
|
![]()
![]()