|
Galton , Francis (1822-1991)
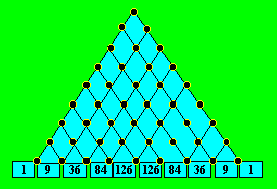
° Planche de Galton.
– Planche imaginée par Galton et qui est couverte de clous disposés selon la
représentation des nombres triangulaires.
Il y a un clou sur la première rangée horizontale, deux sur la deuxième,
trois sur la troisième et ainsi de suite. Les clous sont équidistants sur une
même rangée horizontale et aussi équidistants verticalement. La planche
étant inclinée, on laisse tomber une bille sur le clou du sommet du triangle.
La bille rebondit sur le clou et prend à gauche ou à droite au hasard pour
retomber sur une autre bille inférieure.
Elle continue ainsi son chemin
jusqu'à ce qu’elle tombe dans une des boîtes sous la rangée inférieure de
clous. On se demande alors combien de billes vont se retrouver dans chacune des
boîtes.
Lorsqu’une bille tombe sur un clou, elle a une chance sur deux d’aller à
gauche et une chance sur deux d’aller à droite. Ceci est vrai tout le long du
déplacement.
Par exemple, si on laisse tomber successivement 512 billes sur la
planche ci-haut qui contient neuf rangées horizontales de clous, selon la
probabilité le nombre de billes qui peuvent être trouvées dans chacune des
boîtes est donnée en bas de la planche. Le nombre probable de billes est le
nombre de chemins qui permet d’atteindre la boîte. C’est la 10e
ligne du triangle de Pascal.
© Charles-É. Jean
Index
: G
|
![]()
![]()