° Nombre triangulaire. – Nombre polygonal qui est engendré par un triangle équilatéral. Tout nombre de rang n de cette classe est la somme des n premiers gnomoniques triangulaires ou des n entiers naturels. Le terme général est n(n + 1)/2. Les cinq plus petits triangulaires peuvent être représentés ainsi :

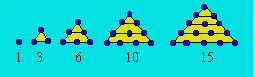
Un nombre est triangulaire si on peut décomposer son octuple en un produit de deux nombres pairs successifs. Son rang est la moitié du plus petit pair.

Pour trouver son successeur, on lui additionne son rang et 1. Par exemple, 253 est un triangulaire car 253 = 22/2 × 23. Il est de rang 22. Son successeur est 253 + 22 + 1 = 276. Les 99 plus petits triangulaires sont :

Un nombre est triangulaire si, en le multipliant par 8 et en additionnant 1 au produit, on obtient un carré. Par exemple, 15 est triangulaire car 15 × 8 + 1 = 11². 

Lorsque le triangulaire est de rang n, le carré est de rang (2n + 1). Pour connaître le rang du triangulaire correspondant à un carré, on retranche 1 à la racine carrée et on divise par 2. Soit le carré 121, on peut écrire (11 - 1) ÷ 2 = 5. D’où, 15 est de rang 5. 

Un nombre triangulaire correspond au nombre de façons de disposer n objets pris deux à deux.

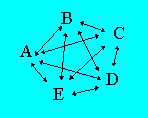
Il y a 10 façons de disposer cinq lettres. Et 10 est un triangulaire de rang 4. Quand on a n objets, le triangulaire de rang (n - 1) est le nombre de façons de les disposer deux à deux.

Voici quelques propriétés concernant les nombres de cette classe :

La période des unités des nombres successifs correspond à un palindrome de 20 chiffres: 01 360 518 655 681 506 310.

Les unités sont 0, 1, 3, 5, 6 et 8.

La somme des n premiers triangulaires est un pyramidal triangulaire de rang n.

La différence de deux triangulaires successifs est un gnomonique triangulaire.

La différence d’un triangulaire de rang n et de son rang est un triangulaire de rang (n - 1).

La somme de deux triangulaires successifs est le carré du rang du plus grand.

La somme de deux triangulaires successifs qu’on multiplie par le rang du plus grand est un cube dont la base est le rang du plus grand. Par exemple, (10 + 15)5 = 125 = 5³.

Le double d'un triangulaire est le produit de son rang par le rang suivant.

L'octuple d'un triangulaire de rang n augmenté de 1 est un carré de rang (2n + 1). (Diophante)

La différence du carré de deux triangulaires successifs est un cube.

Le carré d’un nombre triangulaire est égal à la somme du cube du rang n du triangulaire et du carré du triangulaire de rang (n - 1). Par exemple, 100 = 10² = 4³ + 6². La somme des deux bases est égale à la base du triangulaire.

Neuf fois un triangulaire augmenté de 1 est un triangulaire dont le rang est le triple plus un du rang du premier.

Si t est un triangulaire, alors (9t + 1), (25t + 3), (49t + 6), (81t + 10), ... sont également des triangulaires.

Chaque entier est soit un triangulaire, soit la somme de deux ou de trois triangulaires. (Fermat)

Deux triangulaires successifs dont le premier est pair sont divisibles par un même nombre qui est le rang du plus grand des deux.

Tous les nombres parfaits sont triangulaires.

Deux nombres triangulaires dont la différence de rang est 5 ont la même unité si le plus petit est de rang impair et un chiffre augmenté de 5 si le plus petit est de rang pair.

Deux nombres triangulaires dont la différence de rang est 9 ont le même résidu.

Deux nombres triangulaires dont la différence de rang est 20 ont la même unité.

Les différences successives de deux nombres triangulaires voisins dans une même colonne forment une suite arithmétique dont la raison est 100.

Le produit d’un triangulaire de rang n et de la somme des inverses des n plus petits triangulaires est le carré de n. Par exemple, 4^D(1/1 + 1/3 + 1/6 + 1/10) = 4². 

L’ensemble des triangulaires forme une suite arithmétique de degré 2.

Si on soustrait terme à terme les nombres triangulaires T et les nombres impairs I, on obtient la suite des nombres triangulaires décalée de deux termes. Voici un exemple :

Égalités de triangulaires

On peut trouver des égalités de triangulaires de diverses façons.

Trois triangulaires

Dans ce cas, la somme de deux triangulaires est égale à un triangulaire.

On choisit un entier comme base d’un premier terme. On calcule son triangulaire : c’est le troisième terme. On soustrait 1 : c’est le deuxième terme.

Soit 7 le nombre choisi. Alors, 7^∆ = 28. L’égalité est : 7^∆ + 27^∆ = 28^∆ = 406 où 7^∆ se lit 7 triangulaire ou triangulaire de rang 7.

Quatre triangulaires

La somme de trois triangulaires est égale à un triangulaire.

On choisit un nombre pair 2n comme base d’un premier terme. On additionne 1 : c’est le deuxième terme. On remplace n par sa valeur dans l’expression 2n² + 2n – 1 : c’est le troisième terme. On additionne 2 au dernier terme : c’est le quatrième terme.

Soit 12 le nombre choisi. Alors, n = 6. L’égalité est : 12^∆ + 13^∆ + 83^∆ = 85^∆ = 365

Cinq triangulaires

La somme de deux triangulaires est égale à la somme de trois triangulaires.

On prend 0. On additionne successivement 10, 1 au résultat précédent : ce sont les bases du premier membre de l’égalité. On écrit 3 et on additionne successivement 1, 10 au résultat précédent : ce sont les bases du deuxième membre.

On écrit : 10, 11, puis , 3, 4, 14. L’égalité est : 10^∆ + 11^∆ = 3^∆ + 4^∆ + 14^∆ = 121

Six triangulaires

La somme de trois triangulaires est égale à la somme de trois triangulaires.

On choisit deux entiers de parité différente qui sont les bases des premiers termes de chaque membre de l’égalité. Le plus grand entier est dans le deuxième membre. On additionne 1 aux deux termes choisis : ce sont les deuxièmes termes de chaque membre. On élève au carré chacun de ces résultats et on les soustrait. On additionne 1 et on divise par 2 : c’est un terme du premier membre. On soustrait 3 au carré et on divise par 2 : c’est un terme du deuxième membre.

On choisit 4 et 7. On fait : 4 + 1 = 5, 7 + 1 = 8, 8² – 5² = 39, (39 + 1)/2 = 20 et (39 – 3)/2 = 18. L’égalité est : 4^∆ + 5^∆ + 20^∆ = 7^∆ + 8^∆ + 18^∆ = 235

Additions successives

On peut trouver des égalités de triangulaires par des additions successives.

Huit triangulaires

Cas 1. On choisit un nombre. On fait les opérations indiquées.

On choisit 3. L’égalité est :

3^∆ + 14^∆ + 19^∆ + 30^∆ = 5^∆ + 9^∆ + 24^∆ + 28^∆ = 766

Cas 2. On choisit un nombre. On fait les opérations indiquées.

On choisit 2. L’égalité est :

2^∆ + 18^∆ + 19^∆ + 35^∆ = 5^∆ + 9^∆ + 28^∆ + 32^∆ = 994

Douze triangulaires

Cas 1. On choisit un nombre. On fait les opérations indiquées. 

On choisit 3. L’égalité est :

3^∆ + 8^∆ + 10^∆ + 13^∆ + 15^∆ + 20^∆ = 4^∆ + 6^∆ + 11^∆ + 12^∆ + 17^∆ + 19^∆ = 518

Cas 2. On choisit un nombre. On fait les opérations indiquées.

On choisit 2. L’égalité est :

2^∆ + 12^∆ + 13^∆ + 20^∆ + 21^∆ + 29^∆ = 5^∆ + 6^∆ + 14^∆ + 22^∆ + 23^∆ + 27^∆ = 1048

Carrés magiques d’ordre 3

Dans un carré magique d’ordre 3, la somme des triangulaires des éléments de la première ligne est égale à la somme des triangulaires de la troisième ligne.  Il en est de même pour la première et la troisième colonne.

On peut écrire :

13^D + 2^D + 9^D = 7^D + 14^D + 3^D = 139

13^D + 4^D + 7^D = 9^D + 12^D + 3^D = 129

Carrés magiques d’ordre 4

- Prenons ce carré magique normal dont la densité est 34.

La somme des triangulaires des éléments de la première ligne est égale à la somme des triangulaires des éléments de la quatrième ligne.

2∆ + 8D + 9D + 15D = 3D + 5D + 12D + 14D = 204 .

La somme des triangulaires des éléments du carré central 2 × 2 est égale à la somme des triangulaires des deux premiers éléments de la première colonne et de la quatrième colonne.

1^∆ + 6^∆ + 11^∆ + 16^∆ = 2^∆ + 4^∆ + 13^∆ + 15^∆ = 224

- Prenons ce carré magique non normal qui contient des nombres de 1 à 49 et dont la densité est 100.

La somme des triangulaires des éléments des diagonales brisées partagées en deux parties égales d’une part est égale à la somme des triangulaires des éléments des diagonales brisées partagées de la même façon d’autre part. On peut écrire :

6^∆ + 8^∆ + 42^∆ + 44^∆ = 2^∆ + 14^∆ + 36^∆ + 48^∆ = 1950 

La somme des triangulaires des huit éléments des deux diagonales est égale à la somme des triangulaires des huit éléments apparaissant en périphérie, en excluant les coins. On a :

49^∆ + 37^∆ + 13^∆ + 1^∆ + 7^∆ + 9^∆ + 41^∆ + 43^∆ = 6^∆ + 2^∆ + 14^∆ + 42^∆ + 44^∆ + 48^∆ + 36^∆ + 8^∆ = 3900

Autres considérations
La suite des triangulaires est la même que celle des gnomoniques tétraédriques. Les sept plus petits entiers qui sont en même temps triangulaires et carrés sont : 1, 36, 1225, 41 616, 1 413 721, 48 024 900 et 1 631 432 881. Excepté 1, les deux seuls nombres qui sont à la fois factoriels et triangulaires sont 6 et 120. 

Les triangulaires interviennent dans de nombreux domaines des mathématiques, notamment dans les probabilités et dans l'analyse combinatoire. 

Les triangulaires sont des nombres figurés.

Pour en savoir plus, lisez l'article Quand les oiseaux volent !