Stratégie de résolution d'un problème par laquelle on étend une propriété de proche en proche à tous les termes d'une classe. Le raisonnement basé sur l'examen d'une variété de cas ou d'un ensemble de données permet de passer de faits ou de données à l’établissement d'une loi. Toutefois, cette démarche n'assure pas nécessairement la validité des conclusions. L'induction peut conduire à une conjecture qui peut se révéler fausse à la suite de la découverte d'un contre-exemple. 

Pour s'assurer de la validité des conclusions, il faut se référer à l'induction mathématique qui est un raisonnement par récurrence. L'exemple suivant illustre le danger de faire une conjecture basée sur un nombre restreint de cas : On place successivement deux, trois, quatre et cinq points sur la circonférence d'un cercle. On joint les points deux à deux ; puis, on compte le nombre de régions obtenues. Comment pourrait-on obtenir de régions avec six points ? 

Dans l'illustration suivante, on remarque que le nombre de régions double chaque fois qu'on ajoute un point. On serait donc porté à conclure qu'on peut former 32 régions avec six points et que, de façon générale, le nombre de régions est égal à 2^p-1 où p est le nombre de points.

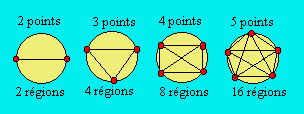
En réalité, on trouve 31 régions avec six points. Le nombre de régions engendrées par p points est égal à n(n - 1)(n - 2)(n - 3)/24 + n(n - 1)/2 + 1. La suite est : 1, 2, 4, 8, 16, 31, 57, 99, 163, 256, 386, 562, etc.

© Charles-É. Jean  

Voir aussi Procéder par induction dans le Lexique de résolution de problèmes.