u Procéder par induction. – Stratégie de résolution de problèmes qui consiste à choisir certaines données d'où on tire des  résultats qui, une fois comparés, permettent d’aboutir à une proposition générale. Cette proposition, qui est alors appliquée au problème donné, peut s’exprimer par une loi ou par une formule. 

Cette stratégie est fragile. La validité des conclusions n’est pas nécessairement assurée. En effet, l'induction conduit parfois à une conjecture qui peut se révéler fausse à la suite de la découverte d'un contre-exemple. 

Pour s'assurer de la validité des conclusions, il faut se référer à l'induction mathématique qui est un raisonnement par récurrence. Cette stratégie en est une d’enchaînement logique.

Problème 1. Combien peut-on compter de carrés de toute grandeur dans une grille 10 × 10 ?

Démarche. On compte le nombre de carrés dans des grilles plus petites. Dans une grille 1 × 1, on compte un carré. Dans une grille 2 × 2, on compte quatre carrés d’une unité et un carré de quatre unités : cinq carrés. Dans une grille 3 × 3, on compte neuf carrés d’une unité, quatre carrés de quatre unités et un carré de neuf unités : 14 carrés. Dans une grille 4 × 4, on compte 16 carrés d’une unité, neuf carrés de quatre unités et quatre carrés de neuf unités et un carré de 16 unités : 30 carrés. Voici un tableau qui montre les résultats précédents :

Quand on passe à une grille plus grande, on augmente d’un carré parfait le nombre de carrés. Ainsi, on a 1 + 4 = 5, 1 + 4 + 9 = 14, 1 + 4 + 9 + 16 = 30. En continuant ainsi, on peut compter 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100 = 385 carrés de toute grandeur dans une grille 10 × 10. On pourrait aussi trouver une formule générale qui est : n(2n² + 3n + 1)/6 dans laquelle n est le nombre d’unités du côté de la grille.

Problème 2. Seize roches sont reliées l'une à l'autre par 22 bouts de ficelle comme ceci:

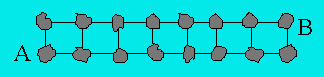
Une mouche part du point A pour se rendre au point B. Elle se dirige toujours de gauche à droite. Toutefois, elle peut aller de haut en bas ou de bas en haut. La mouche doit passer par le plus grand nombre de chemins différents. Combien de chemins la mouche pourra-t-elle emprunter ?

Démarche. S'il y avait une seule rangée verticale de deux roches, la mouche pourrait parcourir un chemin. En ajoutant une rangée, on trouve deux chemins. En ajoutant une autre rangée, on trouve quatre chemins. Puis, en en ajoutant encore une autre, on obtient huit chemins. En voici l'illustration :

Le résultat pour chaque cas est donné par 2 dont la puissance est le nombre de rangées verticales diminué de 1. Pour 16 roches ou 8 rangées, la mouche franchira 2⁷ = 128 chemins.

© Charles-É. Jean

Index : I