Lucas, Édouard (1842-1891)

° Ménages de Lucas. – Récréation posée par le mathématicien français Édouard Lucas (1842-1891) : Des femmes en nombre n sont placées autour d'une table ronde dans un ordre déterminé. De combien de façons leurs maris respectifs pourront-ils s'asseoir de telle manière qu'un homme soit placé entre deux femmes sans se trouver à côté de la sienne ? 

Selon Lucas, le problème revient à trouver le nombre de manières de placer n tours sur l’échiquier de telle manière que ces tours ne puissent pas s’attaquer mutuellement, ne se trouvent pas sur les cases de la diagonale ascendante, ni sur celles de la parallèle immédiatement au-dessus, ni sur le coin inférieur à droite. 

Ce problème fut résolu par le Français Charles-Ange Laisant (1841-1920), par le Français M. C. Moreau, puis par l’Anglais H. M. Taylor. La solution de ce problème s'appuie sur la théorie des permutations discordantes.

Le tableau ci-dessous donne le nombre d'arrangements possibles lorsque le nombre de couples varie de 3 à 9.

Moreau a donné la méthode suivante : À partir de n = 6, pour trouver le nombre intermédiaire de rang n, on multiplie (n - 1) par le nombre intermédiaire de (n - 1). On additionne à ce résultat le nombre intermédiaire de rang (n - 2). On additionne 2 à ce résultat si n est impair et on soustrait 2 s’il est pair. Voici quatre exemples :

si n = 6, on fait : 5 × 3 + 0 - 2 = 13 ;

si n = 7, on fait : 6 × 13 + 3 + 2 = 83 ;

si n = 8, on fait : 7 × 83 + 13 - 2 = 592 ;

si n = 9, on fait : 8 × 592 + 83 + 2 = 4821.

Pour trouver le nombre d’arrangements de n couples, on prend le nombre intermédiaire correspondant à (n + 1) et on y soustrait le nombre intermédiaire correspondant à (n - 1). Par exemple, pour n = 5, on fait : 13 - 0 = 13 ; pour n = 6, on fait : 83 - 3 = 80. Ainsi quatre couples peuvent s’asseoir de deux façons, cinq couples de 13 façons, six couples de 80 façons, etc. 

Voici les deux arrangements possibles lorsqu'il y a quatre couples :

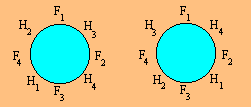
F est mis pour femme et H pour homme. Le problème des ménages de Lucas appartient à la classe des récréations combinatoires. 

© Charles-É. Jean

Index : L