|
Mains
°
Poignées de mains.
– Récréation classique qui illustre la variété des stratégies qui peuvent
être utilisées dans la résolution d'un problème : Dans un groupe de
n personnes, chacune serre la main une et une seule fois à chaque autre.
Combien de poignées de mains seront alors échangées ?
Si n est
petit, on peut résoudre le problème,
soit en faisant faire les gestes appropriés à un nombre
déterminé de personnes et en comptant au fur et à mesure ;
soit en manipulant des objets qui représentent les
personnes ;
soit en dénombrant tous les couples en écrivant les noms
des personnes ou en utilisant des symboles ;
soit en illustrant la situation par un diagramme comme
ci-dessous.
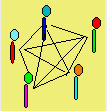
Si n est relativement grand, il est préférable de
procéder par induction ou par déduction. Voici un tableau lorsque n
varie de 2 à 10 :
|
Nombre de personnes |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Nombre de poignées de mains |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
Le nombre de poignées de mains pour n personnes est
égal à n(n - 1)/2. C'est un nombre triangulaire de rang (n
- 1).
Le problème des poignées de mains appartient à la classe des récréations
combinatoires. Pour
en savoir plus, voir les 16 stratégies
mentionnées dans
le Lexique de résolution de problèmes.
© Charles-É. Jean
Index
: M
|
![]()
![]()