u Poignées de mains.  – Certains problèmes peuvent être résolus en faisant un choix parmi plusieurs stratégies. Le problème suivant en est un exemple puisqu’on peut le résoudre par au moins 16 stratégies.

Problème. Douze enfants s'échangent des poignées de mains, chacun à chacun une seule fois. Combien y a-t-il de poignées de mains ?

Démarche. Voici 16 stratégies :
Stratégie 1. Écrire une phrase mathématique. ³ Stratégie d’application
Le 1^er enfant donne 11 poignées, le 2^e en donne 10, le 3^e en donne 9, etc. La phrase mathématique est : 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 66. Il y a 66 poignées de mains.

Stratégie 2. Utiliser une formule. ³ Stratégie d’application
Soit n le nombre d’enfants et m le nombre de poignées, la formule est : m = n(n - 1)/2. Si n = 12, alors m = 12 × 11 ÷ 2 = 66. D’où, 66 poignées.

Stratégie 3. Faire une fausse supposition. ³ Stratégie d’enchaînement logique
On suppose que chaque enfant reçoit 12 poignées de mains : ce qui ferait 12 × 12 ou 144 poignées. Un enfant ne peut pas se donner la main. D’où, 144 - 12 = 132 poignées. Deux mains tendues équivalent à une poignée. D’où, 132 ÷ 2 = 66 poignées.

Stratégie 4. Procéder par analogie. ³ Stratégie d’enchaînement logique
Un élève a déjà résolu le problème : « Huit enfants s’échangent mutuellement des cadeaux. Combien de cadeaux ont été donnés ? » Il avait fait le raisonnement suivant. Chacun des 8 enfants reçoit 7 cadeaux : ce qui fait 8 × 7 = 56 cadeaux. Si l’élève a bien évoqué le problème des poignées, il divisera le produit par 2, car il faut 2 mains pour définir une poignée. Il va donc multiplier 12 par 11 et diviser le résultat par 2 : ce qui donne 66 poignées.

Stratégie 5. Procéder par déduction. ³ Stratégie d’enchaînement logique
Chaque enfant donne 11 poignées. Chaque enfant en reçoit 2. On multiplie 12 par 11 et on divise par 2. Il y a 66 poignées.

Stratégie 6. Utiliser des jetons. ³ Stratégie d’expression physique
On prend 12 jetons. On y écrit 12 noms d’enfants. Pour éviter les erreurs, on procède de façon ordonnée en utilisant le comptage et le calcul. On place les jetons en ligne. On associe le premier jeton à chacun des 11 autres : cela fait 11 contacts. On associe le deuxième jeton à chacun des dix autres de droite : cela fait 10 contacts. On procède selon le même algorithme jusqu’à l’avant-dernier jeton. Il reste à faire la somme des entiers consécutifs de 1 à 11. Il y a 66 contacts ou poignées.

Stratégie 7. Utiliser des objets. ³ Stratégie d’expression physique
Les objets représentent les enfants. On place les objets en ligne. On procède comme dans la stratégie précédente.

Stratégie 8. Vivre la situation en gestes. ³ Stratégie d’expression physique
On place 12 enfants en ligne. On demande au 1^er enfant de donner une poignée à chacun. On procède comme dans les deux stratégies précédentes. On pourrait aussi demander à chaque enfant de la file de compter le nombre de poignées qu’il reçoit. Le 2^e enfant en reçoit 1, le 3^e en reçoit 2 et ainsi de suite.

Stratégie 9. Consulter une table. ³ Stratégie de recherche
Un élève a noté que le nombre de poignées, quand il y a 2, 3, 4, 5, ... enfants, était un nombre triangulaire dont le rang correspond au nombre d’enfants moins l’unité. Il consulte la table des nombres triangulaires et trouve que le 11^e nombre triangulaire est 66. Il y a 66 poignées de mains.

Stratégie 10. Rechercher les combinaisons. ³ Stratégie de recherche
Les enfants sont notés de A à L. On écrit les combinaisons : (A, B), (A, C), (A, D), (A, E), (A, F), (A, G), (A, H), (A, I), (A, J), (A, K), (A, L), (B, C), (B, D), (B, E), etc. On en a 11 qui commence par A, 10 par B, 9 par C, ... etc. Cela donne 66 poignées.

Stratégie 11. Rechercher une formule. ³ Stratégie de recherche
On pose qu’il y a n enfants. Chacun donne (n - 1) poignées de mains. Cela va donner n(n - 1) poignées. Quand un enfant donne et l’autre reçoit, cela compte pour une poignée. Le nombre de poignées est 2 fois trop grand. D’où, il y a n(n - 1)/2 poignées. En remplaçant n par 12, on obtient 66.

Stratégie 12. Rechercher une règle. ³ Stratégie de recherche
Par exemple, il y a 3 enfants. Chaque enfant donne et reçoit 2 poignées : ce qui fait (3 × 2)/2 ou 3 poignées. Par exemple, il y a 4 enfants. Cela fait (4 × 3)/2 ou 6 poignées. Par exemple, il y a 6 enfants. Cela fait (6 × 5)/2 ou 15 poignées. S’il y a 12 enfants, on peut écrire (12 × 11)/2 ou 66 poignées.

Stratégie 13. Construire des modèles. ³ Stratégie de représentation
On trouve le nombre de poignées successivement pour 2, 3, 4 et 5 enfants.

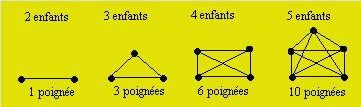
La différence entre le nombre de poignées du 2^e diagramme et du 1^er est 2. La différence entre le nombre du 3^e diagramme et du 2^e est 3. La différence entre le nombre du 4^e diagramme et du 3^e est 4. À chaque fois qu’un enfant s’ajoute, le nombre de poignées augmente du nombre précédent d’enfants. D’où, les autres termes de la suite seront : 15, 21, 28, 36, 45, 55, 66. Il y a 66 poignées de mains.

Stratégie 14. Construire un graphique. ³ Stratégie de représentation
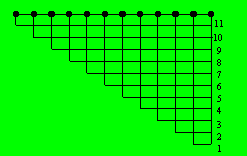
Chaque enfant est représenté par un point. Les points d’intersection représentent les poignées de mains. Il reste à additionner les nombres de 1 à 11. Il y a 66 poignées de mains.

Stratégie 15. Construire un tableau. ³ Stratégie de représentation

Pour 2 enfants, le nombre de poignées de mains est 1.
Pour 3 enfants, ce nombre est 1 + 2.
Pour 4 enfants, ce nombre est 1 + 2 + 3.
Pour 5 enfants, ce nombre est 1 + 2 + 3 + 4.
Pour 12 enfants, il sera : 1 + 2 + 3 + 4 + ... + 10 + 11 = 66.

Stratégie 16. Décomposer en sous-problèmes. ³ Stratégie de représentation
On partage les enfants en deux groupes de six enfants. À l’intérieur de chaque groupe, 15 poignées sont données. Les enfants des deux groupes se donnent la main. Cela fait 6 × 6 = 36 poignées. Il y a (2 × 15 + 36) ou 66 poignées de mains.