° Nombre multicyclique. – Entier naturel de n chiffres qui, multiplié par certains entiers, engendre des nombres qui ont les mêmes propriétés qu'un nombre cyclique. En multipliant chacun d'eux par certains entiers, on obtient des produits qui contiennent les mêmes chiffres dans un même ordre cyclique. Ainsi, 76 923 est un nombre multicyclique ; il engendre deux nombres qui produisent des cycles : 076 923 et 153 846. Le nombre 76 923 correspond à la période de 1/13. 

Outre 1/13, les fractions 1/31, 1/43, 1/67, 1/71, 1/83 et 1/89 permettent deux cycles. Par ailleurs, 2439 engendre huit cycles : 02 439, 04 878, 07 317, 09 756, 12 195, 14 634, 26 829 et 36 585. Ils correspondent respectivement à la période des fractions 1/41, 2/41, 3/41, 4/41, 5/41, 6/41, 11/41 et 15/41. 

La représentation des nombres 02 439, 04 878 et 07 317 sous forme d'horloge est donnée ci-dessous. Chaque nombre extérieur au cadran marque le départ d'un cycle à l'intérieur et est le numérateur d'une fraction dont le dénominateur est 41.

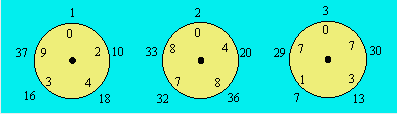
Dans un nombre multicyclique, les cycles sont toujours de même longueur. Soit une fraction 1/n engendrant des nombres cycliques, le produit du nombre de cycles et du nombre de chiffres par cycle est égal à (n - 1).

© Charles-É. Jean

Index : M