|
Cyclique
° Nombre cyclique.
– Entier naturel de n
chiffres qui, multiplié par tout entier inférieur à n, engendre un
produit qui contient les mêmes chiffres dans un même ordre cyclique. On
accepte un ou des zéros au début du nombre puisque ceux-ci apparaissent dans d’autres
positions.
Le nombre 142 857 est cyclique. Il correspond à la période
de 1/7. Multiplié par 2, 3, 4, 5 et 6, on obtient respectivement d’autres
nombres cycliques : 285 714, 428 571, 571 428, 714 285 et 857 142. Les chiffres
de ces nombres sont 1, 4, 2, 8, 5 et 7 dans l'ordre cyclique. Voici
l'illustration du cycle :
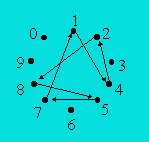
La période des fractions dont le dénominateur est
successivement 7, 17, 19, 23, 29, 47, 59, 61 et 97 donne des nombres cycliques.
Voici le nombre cyclique correspondant à six fractions dont les
dénominateurs sont des nombres premiers :
|
Fraction |
Période/
Nombre cyclique |
|
1/7 |
142 857 |
|
1/17 |
0 588 235 294 117 647 |
|
1/19 |
052 631 578 947 368 421 |
|
1/23 |
0 434 782 608 695 652 173 913 |
|
1/29 |
0 344 827 586 206 896 551 724 137 931 |
|
1/47 |
0 212 765 957 446 808 510 638 297 872 340 425 531 914 893 617 |
Si on multiplie chacune des périodes de ce tableau par le dénominateur de
la fraction, le produit est un nombre formé uniquement de chiffres 9.
Les
nombres cycliques ont un nombre de chiffres inférieur d'une unité au
dénominateur de la fraction.
La théorie des nombres cycliques s'appuie sur le
développement d'un nombre décimal périodique. On peut trouver des nombres
cycliques par la multiplication à
rebours. On ne connaît pas de formule permettant de tous les
connaître. On ne sait pas s'il en existe une infinité.
Tout nombre cyclique
est conservateur et circulaire.
© Charles-É.
Jean
Index
: C
|
![]()
![]()