° Nombre pensé. – Nombre choisi par une personne et qui doit être deviné par une autre. Des opérations successives sont indiquées et le résultat final ou non peut permettre de deviner le nombre choisi. Dans certains cas, des questions peuvent être posées pour savoir, par exemple, si le nombre pensé est pair ou impair. Parfois, le choix de plus d'un nombre au départ est requis. 

Des objets numérotés comme des jetons ou des cartes peuvent être utilisés. Le calcul algébrique permet de créer de nombreuses récréations de cette classe. 

Dans les siècles passés, les nombres pensés ont eu une place importante dans la littérature récréative, d'autant plus qu'ils peuvent être, avec des variantes, la base de tour de magie. Voici sept exemples :

1. On dit à la personne : Pensez à un nombre. Multipliez-le par 6. Additionnez 42. Divisez le résultat par 3. Soustrayez 20. Divisez le résultat par 2. Quel est le résultat ?

Il s’agit d’additionner 3 au résultat pour trouver le nombre pensé. Pour ne pas que la personne devine le truc, on peut modifier certaines opérations à la condition de connaître au préalable la relation entre le résultat et le nombre pensé.

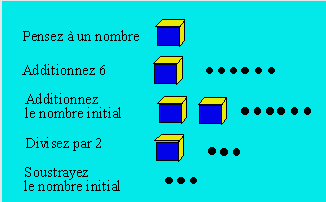
2. On dit à la personne : Pensez à un nombre. Additionnez 6. Additionnez le nombre initial. Divisez le résultat par 2. Soustrayez le nombre initial. Quel est le résultat ?

On n’a pas besoin de demander à la personne son résultat car celui-ci est toujours 3. Ci-après, on donne la séquence d'opérations et leur représentation visuelle à l'aide d'une boîte et des billes. Le nombre pensé correspond au nombre de billes sans tenir compte de la boîte.

3. Faites tripler le nombre pensé. Faites prendre la moitié du résultat obtenu, exactement si c’est possible, sinon on fera ajouter 1 au quotient. Faites tripler le nouveau résultat obtenu et qu’on vous annonce le résultat définitif. Vous divisez alors par 9 ce nombre définitif. Le nombre pensé sera le double du quotient, sauf s’il a fallu ajouter 1 dans la seconde opération ; dans ce dernier cas, vous ajouterez également 1. Nicolas Chuquet (1450-1488)

Par exemple, le nombre pensé est 35. La personne fait : 35 ´ 3 = 105, 105 ¸ 2 = 52 reste 1, 52 + 1 = 53, 53 ´ 3 = 159. Vous faites 159 ¸ 9 = 17 reste 6, 17 ´ 2 + 1 = 35.

4. Faites multiplier le nombre pensé par lui-même. Faites augmenter le nombre pensé d’une unité et multiplier le nombre obtenu par lui-même. Faites effectuer la différence des deux carrés. Connaissant cette différence qui est toujours un nombre impair, en la diminuant de 1, on a le double du nombre cherché. Jacques Ozanam (1640-1717)

Par exemple, le nombre pensé est 26. La personne fait 26 ´ 26 = 676, 27 ´ 27 = 729, 729 - 676 = 53. Vous faites : 53 - 1 = 52 et 52 ¸ 2 = 26.

5. Faites penser à un nombre. Faites-le multiplier par 3. Faites retrancher 1 du produit obtenu et multiplier le résultat obtenu par 3. Faites ajouter le nombre pensé au dernier produit obtenu. Demandez le résultat, ajoutez-lui 3 mentalement ; le résultat est un nombre exact de dizaines, supprimez le zéro (chiffre des unités) et vous avez le nombre pensé. Gaston Boucheny (1865-1935)

Par exemple, le nombre pensé est 52. La personne fait 52 ´ 3 = 156, 156 - 1 = 155, 155 ´ 3 = 465, 465 + 52 = 517. Vous faites : 517 + 3 = 520. On supprime le 0.

6. On peut aussi deviner un nombre en utilisant quatre cartes sur lesquelles on a préalablement inscrit des nombres. Voici un ensemble de quatre cartes :

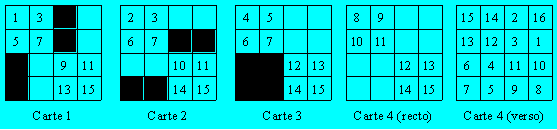
Dans la confection de la carte 4, on écrit 16 vis-à-vis 8, 2 vis-à-vis 9 et ainsi de suite On place d’abord les quatre cartes dans l’ordre, la carte 1 étant au-dessus. On demande à une personne de choisir un nombre de 1 à 16. On lui montre les quatre cartes, le recto pour la carte 4, et on lui demande de dire si, oui ou non, le nombre choisi apparaît sur la carte désignée. Pour les trois premières cartes, quand la personne dit oui, on ne fait que glisser la carte sous le paquet. Quand la personne dit non, en plus de glisser la carte, on lui fait faire un tour de 180°. On laisse la carte 4 sur le paquet. Si le nombre y apparaît, on fait tourner la carte de 180°; sinon, on tourne la carte de 90° vers la droite. On retourne le paquet et le nombre choisi apparaît seul dans une fenêtre.

7. De plusieurs nombres par ordre commençant par l’unité et disposés en rond, deviner lequel on aura pensé. Soit par exemple les nombres de 1 à 12.

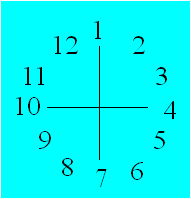
Au nombre touché ajoutez le plus grand nombre du cercle, et dites à la personne qu’à partir du nombre qu’elle touche, inclusivement, elle compte à rebours sur le cercle depuis le nombre qu’elle a pensé jusqu’à la somme que vous avez obtenue, et en touchant à mesure chacun des nombres du cercle : le nombre sur lequel elle s’arrêtera sera le nombre pensé. Extrait de Problèmes plaisants et délectables qui se font par les nombres de Claude-Gaspard Bachet de Méziriac (1581-1638), 3^e éd., 1874, p. 86

Voici un exemple dans lequel on écrit les nombres de la figure en lettres : La personne pense à 10. Elle touche à TROIS (3). Vous faites 3 + 12 = 15. Sans mentionner l’opération faite, vous dites à la personne de toucher à TROIS et de compter les nombres jusqu'à 15 dans l’ordre inverse de la suite. La personne commence à compter comme si elle était au rang 10, soit son nombre pensé. Elle compte 10 (TROIS), 11 (DEUX), 12 (UN), 13 (DOUZE), 14 (ONZE), 15 (DIX). Au rang 15, on trouve DIX. Le nombre pensé est 10. Dans un tour de magie, on peut additionner mentalement un autre nombre que 12. Dans ce cas, lors de l’arrêt, on corrigera mentalement l’opération de comptage et on dira à la personne : Non, ce n’est pas le nombre auquel tu as pensé, c’est plutôt ... On peut remplacer les nombres par des objets numérotés comme des cartes ou encore on peut choisir une autre suite.